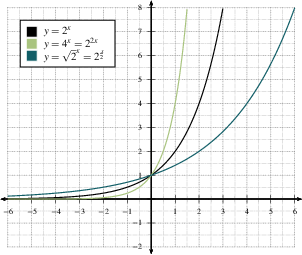
There is no answer available Request an answer from our educators and we will get to it right away!In this video I want to introduce you to the idea of an exponential function exponential function and really just show you how fast these things can grow so let's just write an example exponential function here so let's say we have Y is equal to 3 to the X power notice this isn't X to the 3rd power this is 3 to the X power our independent variable X is the actual exponent so let's make a tableExponential function determined by a point Drag the point (1, 2) to update In general, equations involving exponential functions are easier to graph than polynomial equations because the exponential functions themselves are easy to graph Exercise 1 Sketch the graphs of y = 2 x, y = 2 x 3, and y = 2 x 3 2 in the same coordinate plane
Exponential And Logarithmic Functions Exponential Functions Sparknotes
Graph the exponential function y=5(2)^x quizlet
Graph the exponential function y=5(2)^x quizlet-👉 Learn how to convert an exponential equation to a logarithmic equation This is very important to learn because it not only helps us explain the definitiSection 63 Exponential Functions 307 STUDY TIP The graph of y = abx approaches the xaxis but never intersects it Graphing Exponential Functions The graph of a function y = abx is a vertical stretch or shrink by a factor of ∣ a ∣ of the graph of the parent function y = bxWhen a < 0, the graph is also refl ected in the xaxisThe yintercept of the graph of y = abx is a



Transforming Exponential Graphs Example 2 Video Khan Academy
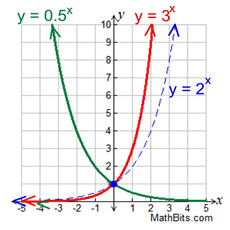
The base b of an exponential function affects the rate at which it grows Below we have graphed y = 2x, y = 3x, and y = 10x on the same set of axes Note that all of these exponential functions have the same y intercept, namely (0, 1) This is because f(0) =Nov 26, 16 · An exponential function is a mathematical function of the following form f ( x ) = a x where x is a variable, and a is a constant called the base of the functionThe most commonly encountered exponentialfunction base is the transcendental number e , which is equal to approximately 2718 Thus, the above expression becomesApr 06, · Exponential growth happens when things multiply repeatedly, as when each person can spread a rumor, or a disease, to several other people at a time Now the increase is increasing even faster 1, 2, 4, doubling the increase each time, just as the function itself does
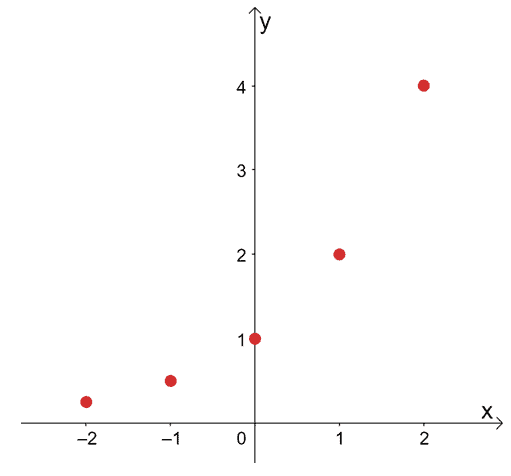
Graph an Exponential Function y=2x x Y=2x 3 23=1/8 2 22=1/4 1 21=1/2 0 =1 1 21=2 2 22=4 3 23=8 Domain all real #s Range all positive #s What is an Exponential Function?The formula is y= abx when a≠0, b>0, b≠1 it is continuous and "one and one" meaning it has to beFind the Asymptotes y=2^x y = 2x y = 2 x Exponential functions have a horizontal asymptote The equation of the horizontal asymptote is y = 0 y = 0 Horizontal Asymptote y = 0 y = 0
Exponential functions are sometimes known as growth or decay curves A spreadsheet can be used to investigate this type of function eg For the function y = 2 x • As x gets smaller, y gets smaller and closer to the xaxis The xaxis is an asymptote • As x gets larger, y gets larger • This is the shape of the graph of an exponentialExponential Functions An exponential function is just one of the different types of functions An exponential function is a function in the form {eq}f(x)=a\cdot b^x {/eq} where a is the yinterceptOct 17, · FileExponential function y = 2^xsvg Size of this PNG preview of this SVG file 315 × 255 pixels Other resolutions 297 × 240 pixels 593 × 480 pixels 741 × 600 pixels 949 × 768 pixels 1,265 × 1,024 pixels


Graphing Exponential Functions It Is Important To Know The General Nature And Shape Of Exponential Graphs The Actual Values That May Be Plotted Are Relatively Few And An Understanding Of The General Shape Of A Graph Of Growth Or Decay Can Help Fill In The
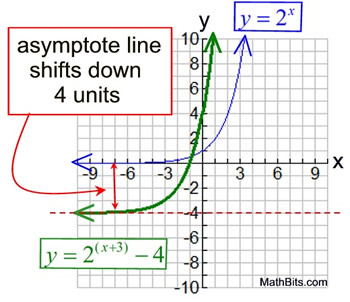


Exponential Functions Mathbitsnotebook Ccss Math
And so this is clearly an exponential function right over here Let's think about the behavior as x is, when x is very negative, or when x is very positive When x is very negative, three to a very negative number like let's say you had three to the negative 3rd power, that would be 1/27th, or three to the negative 4th power, that would be 1/81stJun 06, 15 · Jun 7, 15 No, this is a quadratic function Graphically it will give you a Parabola graph {x^21 10, 10, 5, 5} To have an exponential, the variable x must appear as an exponent of some number a for example ax Have a look Answer linkGiven the exponential function y = − 2 ( 3) x 5 y=2\left (3\right)^x5 y = −2(3)x 5 , please find the value of y when x = 6 x=6 x = 6 answer choices y = − 1453 y=1453 y = −1453 y = 4997
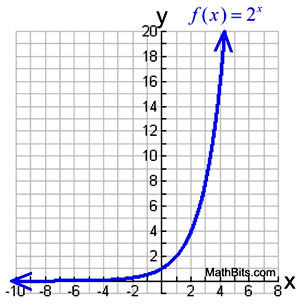


Exponential Functions Mathbitsnotebook Ccss Math



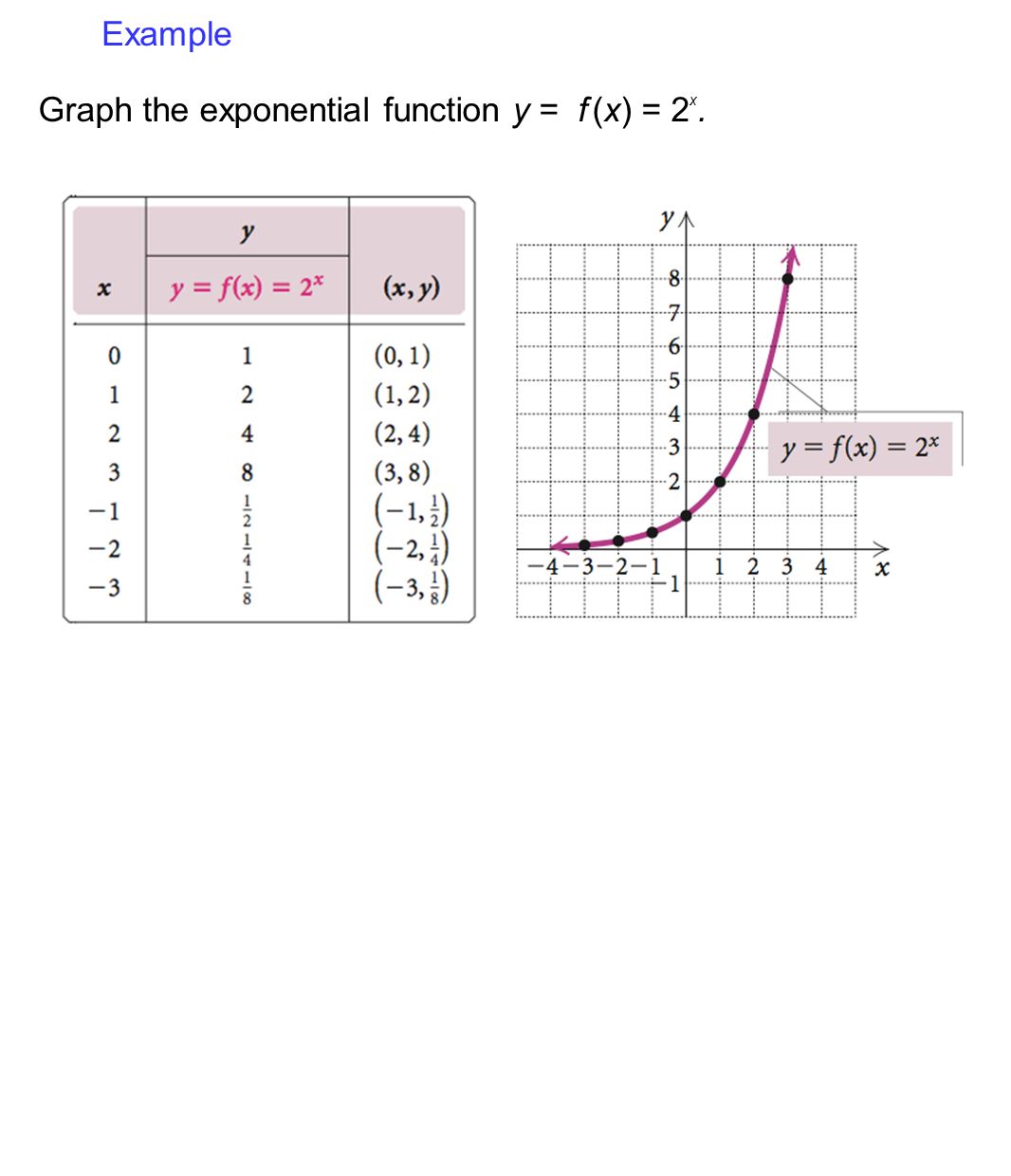
Example 2 Graph An Exponential Function Graph The Function Y 2 X Identify Its Domain And Range Solution Step 1 Make A Table By Choosing A Few Values Ppt Download
In addition to linear, quadratic, rational, and radical functions, there are exponential functions Exponential functions have the form f(x) = b x, where b > 0 and b ≠ 1 Just as in any exponential expression, b is called the base and x is called the exponent An example of an exponential function is the growth of bacteriaPrecalculus Exponential and Logistic Functions Example Sketch y= ae kxwhere a>0 and k>0 are real numbers Basic Function y= f(x) = ex y= f( x) = e xre ect about yaxis y= f( kx) = e kxhorizontal compression by factor of k y= af( kx) = ae kxvertical stretch by a factor of a From the sketch we can analyze the behaviour of the function f(x) = ae kxwhere a>0 and k>0There is no answer available Request an answer from our educators and we will get to it right away!



Graphing Exponential Functions
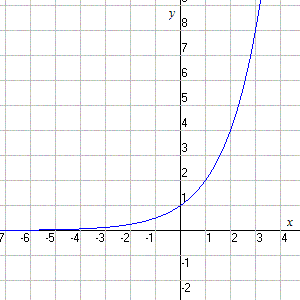


Exponential Functions
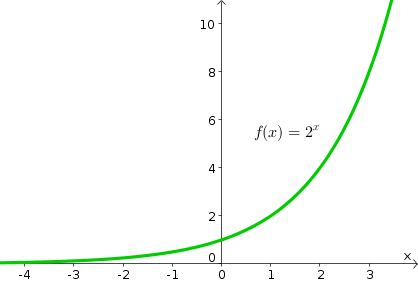
Learn termexponential function = y = 2^x with free interactive flashcards Choose from 500 different sets of termexponential function = y = 2^x flashcards on QuizletOther examples of exponential functions include y = 3 x f (x) = 45 x y = 2 x 1 The general exponential function looks like this y = b x, where the base b is any positive constant The base b could be 1, but remember that 1 to any power is just 1, so it's aExponential Functions The "basic" exponential function is the function y = a x where a is some positive constant For example, the graph of y = 2 x looks like this Note that 1 ) The y intercept is 1 (no matter what the value of a is)
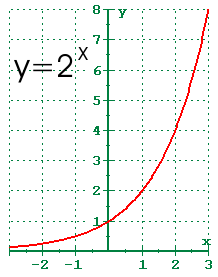


4 1 Exponential Functions And Their Graphs
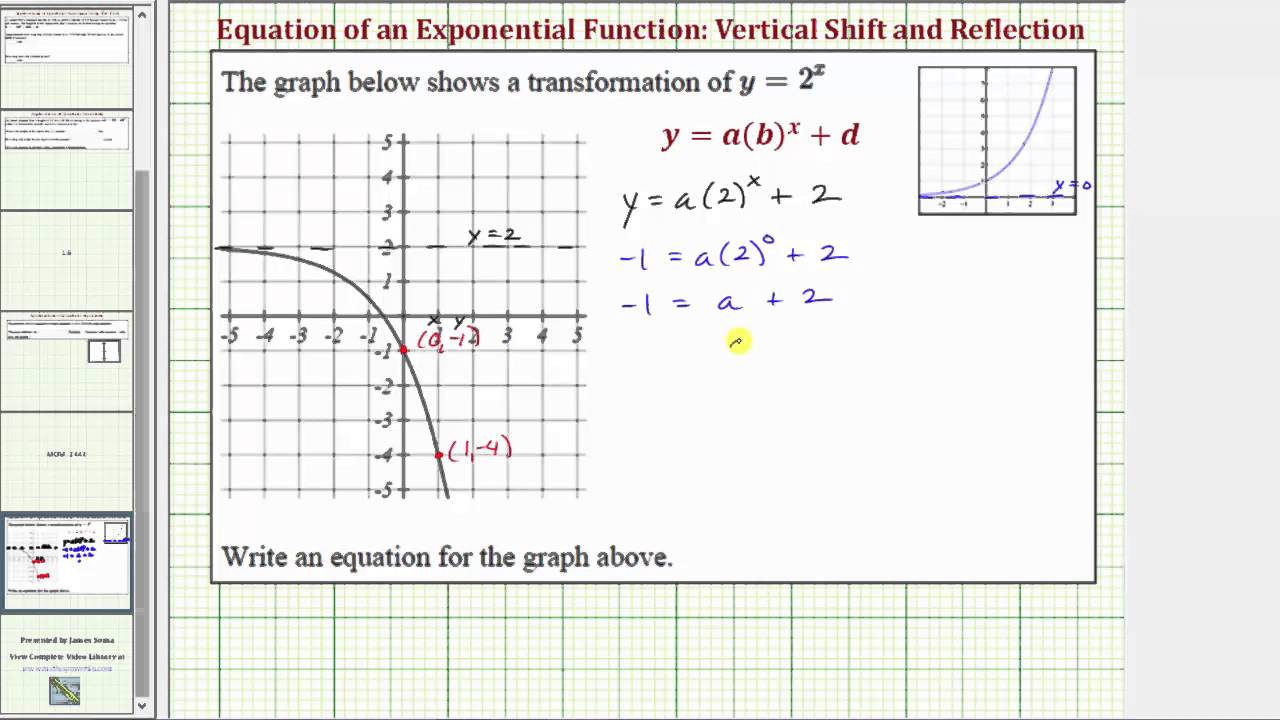


Ex Determine The Equation Of A Transformation Of Y 2 X Youtube
Dec 18, · This means that the function almost "dies out" (the values get closer and closer to 0) as t approaches \(−\infty\) What about the graphs of other exponential functions with different bases?Exponential decay Another application of exponential functions is Exponential decay If k is positive, the graph of g(x) = ekx has the familiar exponential function explosion seen in the earlier graph of f(x) = 2x (Indeed, if k ˇ 0693, the curves y = 2x and y = ekx are the same) But what if k is negative?SOLVEDGraph each exponential function y=2^ {x}3 Problem Graph each exponential function $$ y=\left (\fra Uh oh!


Untitled Document


Bestmaths
Solve equations involving exponential and logarithmic functions Finally, some applications are looked at 1 Exponential Functions 11 Definitions Examples Definition 1 (Exponential Function) 1 An exponential function is a function of the form y = f (x)=bx 2 b is called the base of the exponential It will always be strictly positive,Hint recall the equation y=a (b) x b (The common ratio) 100 This is the formula for exponential transformations What is y = a (b) (xh) K 100An exponential function is a function of the form f (x) = a ⋅ b x, f(x)=a \cdot b^x, f (x) = a ⋅ b x, where a a a and b b b are real numbers and b b b is positive Exponential functions are used to model relationships with exponential growth or decay Exponential growth occurs when a


Solution A Construct A Table Of Values For The Exponential Function Y 2 3 X Use Values Of X From 1 To 3 B Graph The Equation Connect The Points With A Solid Line C What
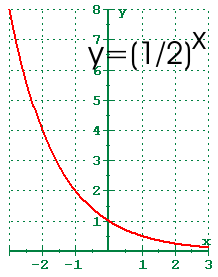


4 1 Exponential Functions And Their Graphs
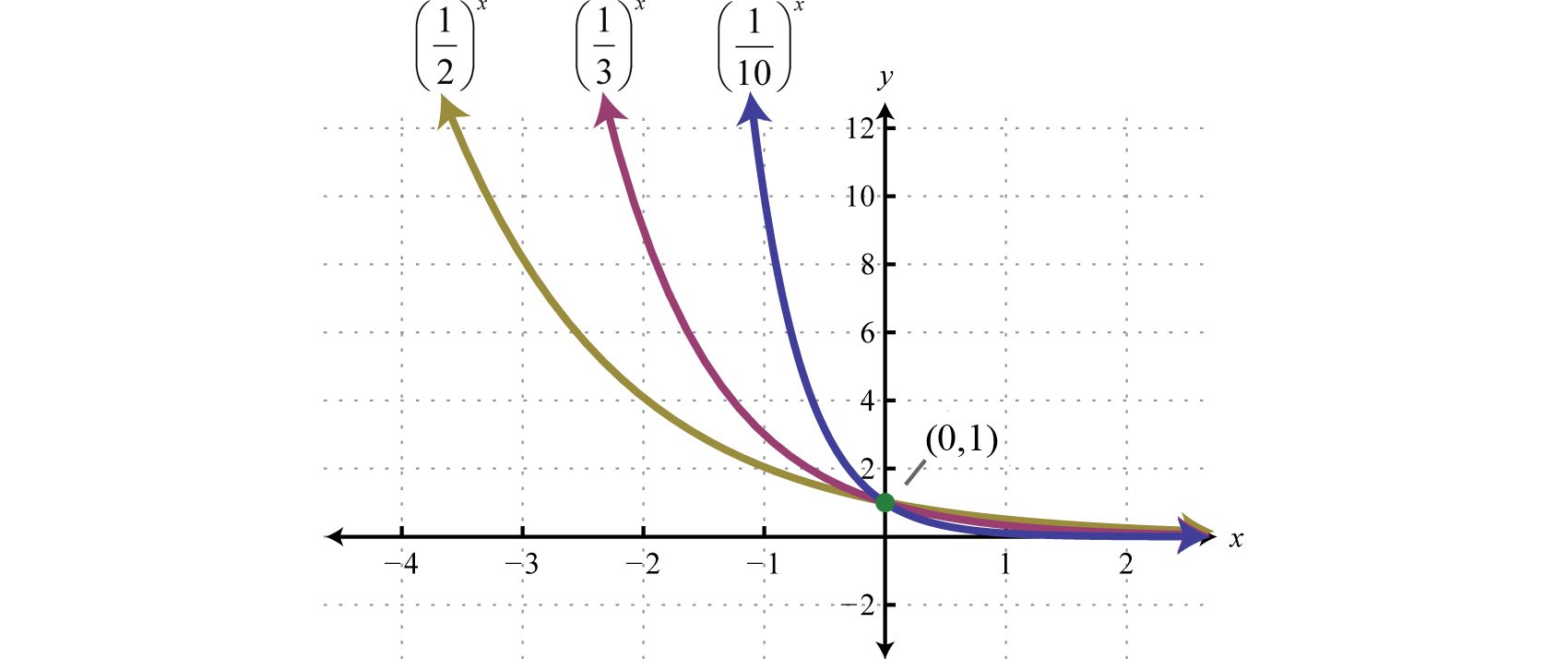
SOLVEDGraph each exponential function y=3^ {x}1 Problem Answer the questions about the graph of y = 2 x Uh oh!To get a sense of the behavior of exponential decay, we can create a table of values for a function of the form f(x) = bx f ( x) = b x whose base is between zero and one We'll use the function g(x) = (1 2)x g ( x) = ( 1 2) x Observe how the output values in the table below change as the input increases by 1 xThe exponential graph of a function represents the exponential function properties Let us consider the exponential function, y=2 x The graph of function y=2 x is shown below First, the property of the exponential function graph when the base is greater than 1 Exponential Function Graph for y=2 x The graph passes through the point (0,1)



6 2 Exponential Functions Objectives Classify An Exponential
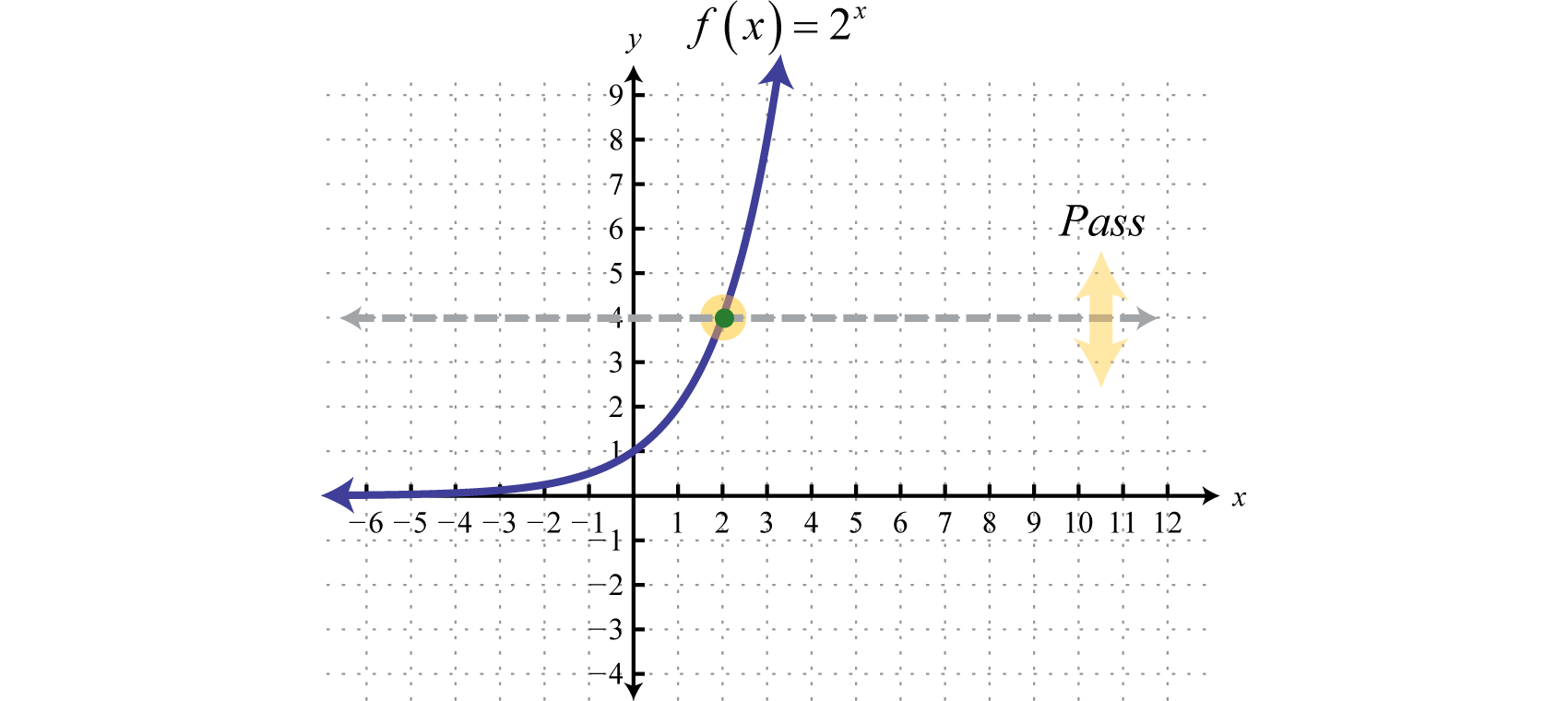


Logarithmic Functions And Their Graphs
Derivatives of Exponential Functions On this page we'll consider how to differentiate exponential functions Exponential functions have the form f\left ( x \right) = {a^x}, f ( x) = a x, where a a is the base The base is always a positive number not equal to 1By making this transformation, we have translated the original graph of y = 2 x y=2^x y = 2 x up two units If "k" were negative in this example, the exponential function would have been translated down two units "k" is a particularly important variable, as it is also equal to what we call the horizontal asymptote!Jan 13, 21 · Graph the function y=2 x Use a table to help Example 1 Solution The most important things to identify when graphing an exponential function are the yintercept and the horizontal asymptote We know that for any function a x, the horizontal asymptote is the xaxis, y=0 Since there is not vertical shift in this function (that is, no numbers
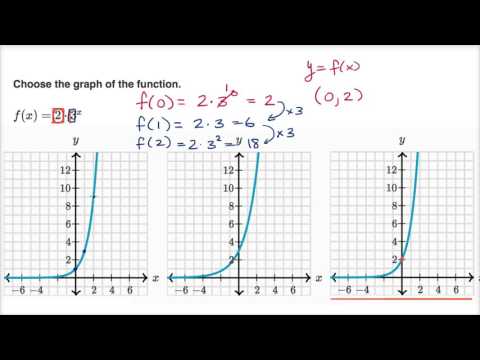


Graphs Of Exponential Growth Video Khan Academy



How To Find Equations For Exponential Functions Studypug
The graph of g(x) = e x is re ectedAug 05, 15 · In an exponential function, the independent variable, or xvalue, is the exponent, while the base is a constant For example, y = 2 x would beExponential / Logarithm Unit Test Review Name_____ ID 1 Date_____ Period____ ©M d2Y0\2p1r vKOuytEa eSXoQfVtjwKajr_ek JLbLMCjm o qAElclX SrCiHgIhftlsT jrJeuskeeravQeds1Graph each function State the Domain & Range 1) y = 3x x y 2 4 6 8 2) y = (1 3) x x y 642 2 4 6 8
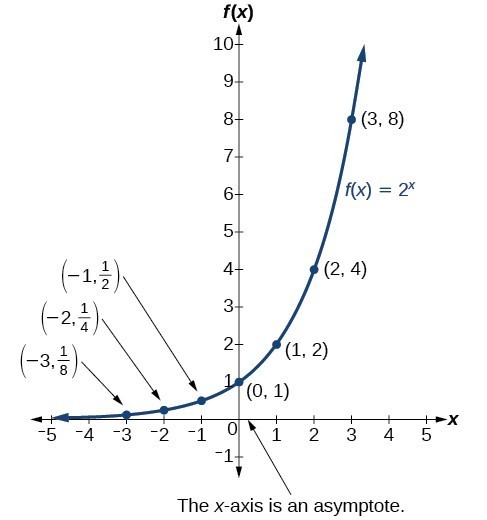


Characteristics Of Graphs Of Exponential Functions College Algebra



Graphs Of Exponential Functions
Free quadratic equation calculator Solve quadratic equations using factoring, complete the square and the quadratic formula stepbystepRequest Answer Input your name and email to request the answerWe'll use the calculator to explore several of these First, use your calculator to compare \(y_{1}(x) = 2^x\) and \(y_{2}(x) = 3^x\)


Logarithmic And Exponential Graphs


Content How Fast Does An Exponential Function Grow
Jun 02, 18 · Let's start off this section with the definition of an exponential function If b b is any number such that b > 0 b > 0 and b ≠ 1 b ≠ 1 then an exponential function is a function in the form, f (x) = bx f ( x) = b x where b b is called the base and x x can be any real number Notice that the x x is now in the exponent and the base is aAn exponential function has the form f(x) =abx, where b> 0 and b≠ 1, a ≠ 0 f ( x) = a b x, where b > 0 and b ≠ 1, a ≠ 0 Quantities that increase or decrease by a constant percent in each time period grow or decay exponentially 🔗 Properties of Exponential Functions f(x) =Exponential functions are growth functions when which variable is greater than 1?


File Exponential Function Y 2 X Svg Wikimedia Commons
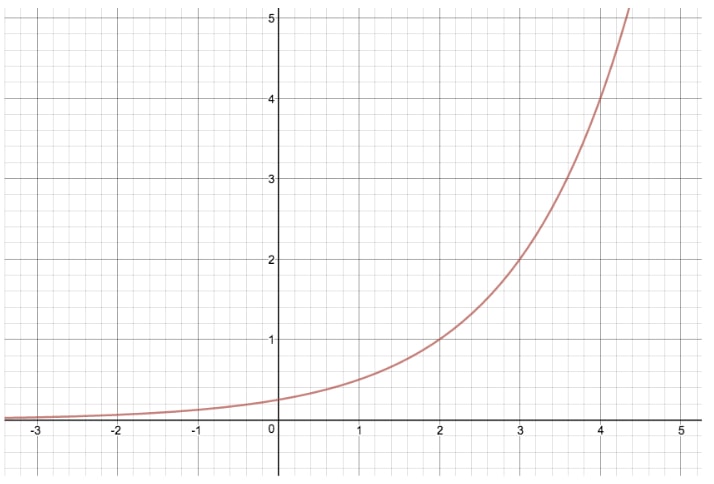


How To Find Equations For Exponential Functions Studypug
The domain of the function is (−∞,∞) The range of the function is (−2,∞) The Natural Base e The irrational number e appears in many applications and is called the natural base The exponential function with base e ( )= 𝑥 is called the exponential function or the natural exponential function 0 10 30 40 50 60 704 2 0 2 4 yRequest Answer Input your name and email to request the answerQ Write the equation of the function Q Determine whether each table or rule represents a linear or an exponential function Q Write the equation of the function Q State the domain of the exponential function Q Describe the change in the graph from y= 4 x to y=4 x 3


Transforming Exponential Functions



Roll Some Excitement Into Your Math Classroom With The Exponential Function Transformations Board Game Algebra Worksheets Exponential Functions Functions Math
Section 23 Exponential Functions An exponential function is a function of the form \(f(x)=a^x\text{,}\) where \(a\) is a constant Examples are \(2^x\text{,}\) \(10^x\) and \((1/2)^x\text{}\) To more formally define the exponential function we
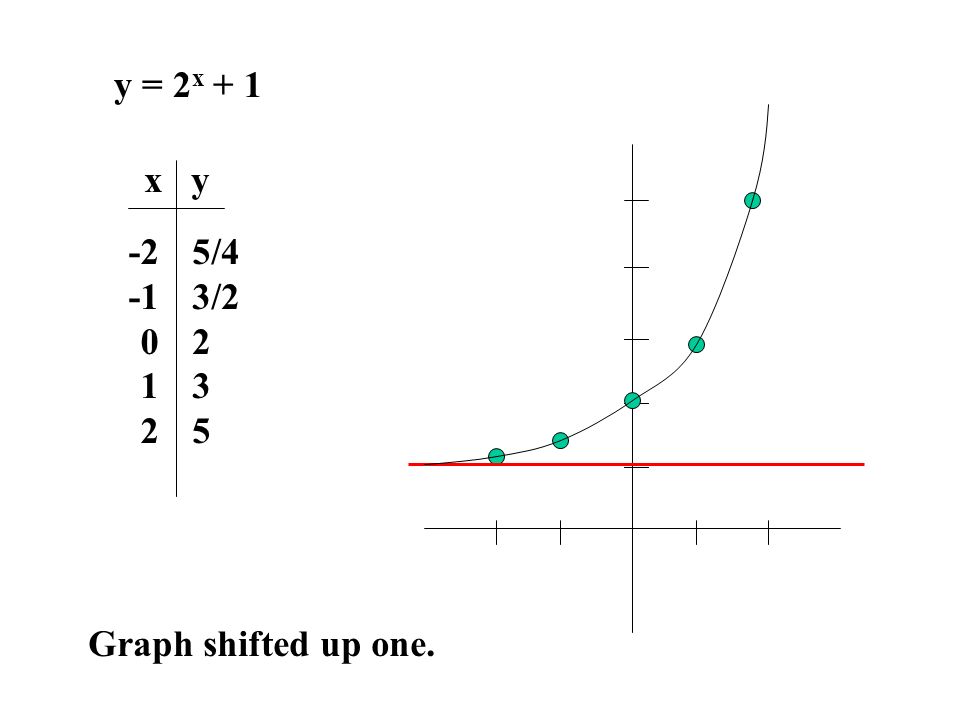


3 1 Exponential Functions And Their Graphs The Exponential Function F With Base A Is Denoted By F X A X And X Is Any Real Number Ppt Download



How To Find Equations For Exponential Functions Studypug
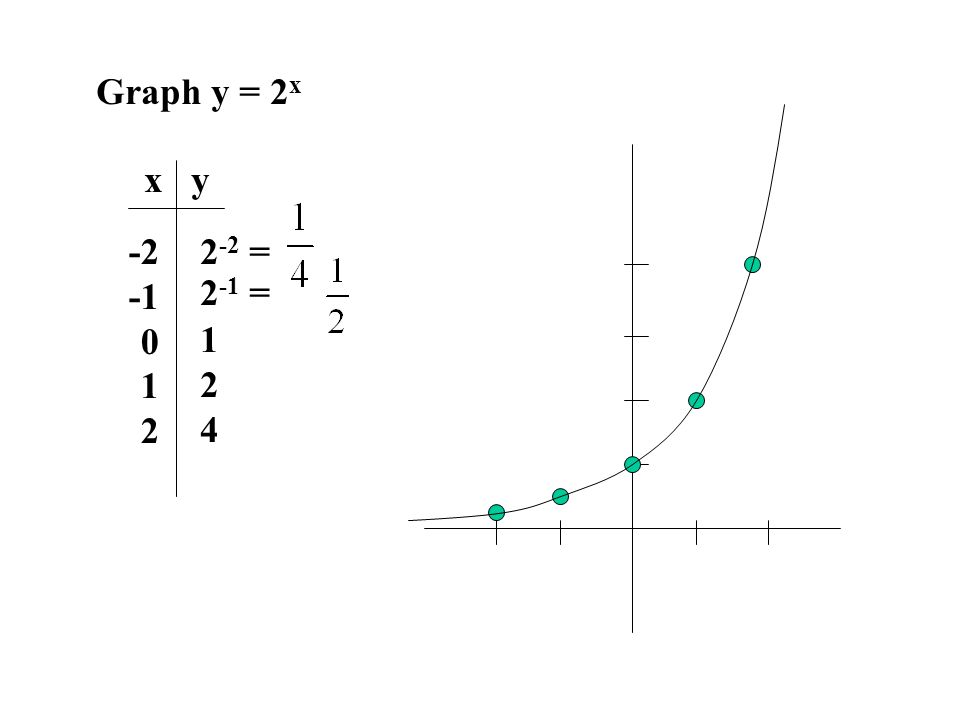


3 1 Exponential Functions And Their Graphs The Exponential Function F With Base A Is Denoted By F X A X And X Is Any Real Number Ppt Download



Graphs Of Exponential Functions Ck 12 Foundation



How To Find Equations For Exponential Functions Studypug


Exponential Functions Introduction
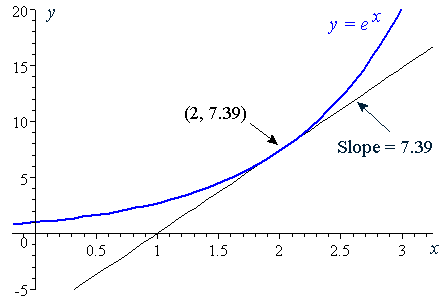


6 Derivative Of The Exponential Function



How Do You Find The Horizontal Asymptotes Of A Function Magoosh Blog High School


Solved Y 2 4 5 Graph The Exponential Function Chegg Com
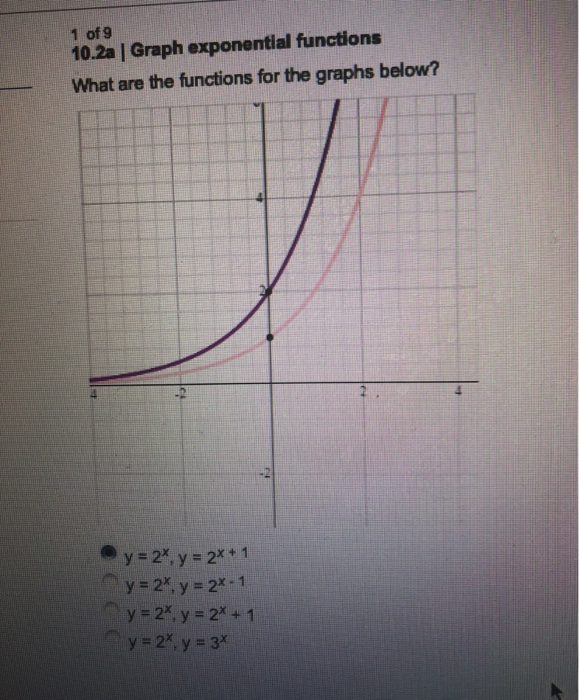


Solved 1 Of 9 10 2a Graph Exponential Functions What Ar Chegg Com



Exponential Functions Quick Check And Warm Up Template Exponential Functions Functions Algebra Math Template
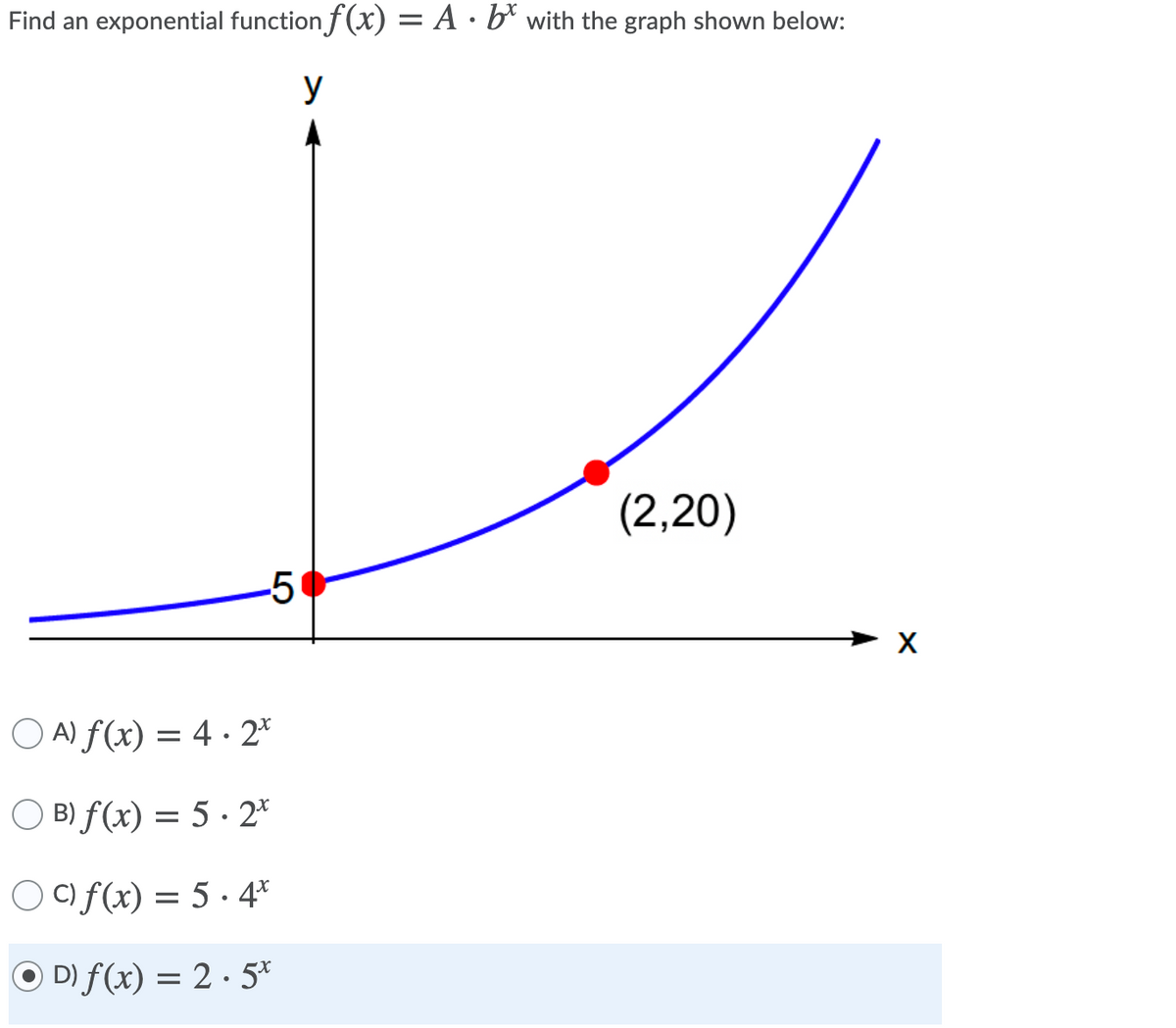


Answered Find An Exponential Function F X A Bartleby



Timed 30pts The Graphs Of The Quadratic Function Y 2x 2 And The Exponential Function Y 2 X Are Brainly Com



File Exponential Function Y 2 X Svg Wikimedia Commons


Exponential And Logarithmic Graphs



Transforming Exponential Graphs Example 2 Video Khan Academy


Graph Exponential Functions Using Transformations College Algebra


Exponential And Logarithmic Functions Exponential Functions Sparknotes


Functions Exponential Functions



Let S Learn Exponential Functions And Their Graphs


Exponential Functions


Exponential Functions And Their Graphs


Exponential And Logarithmic Functions And Equations Ppt Download



The Exponential Function Math Insight


Introduction To Exponential Functions
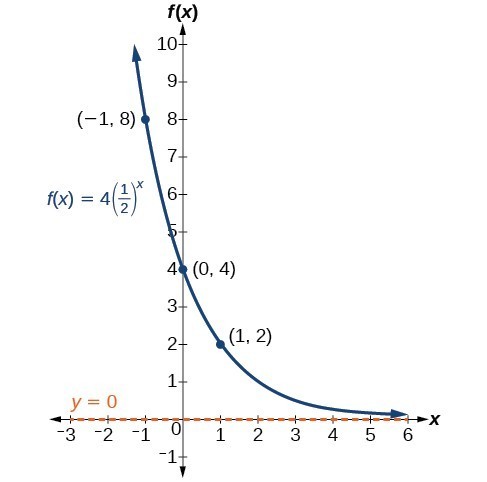


Graph Exponential Functions Using Transformations College Algebra
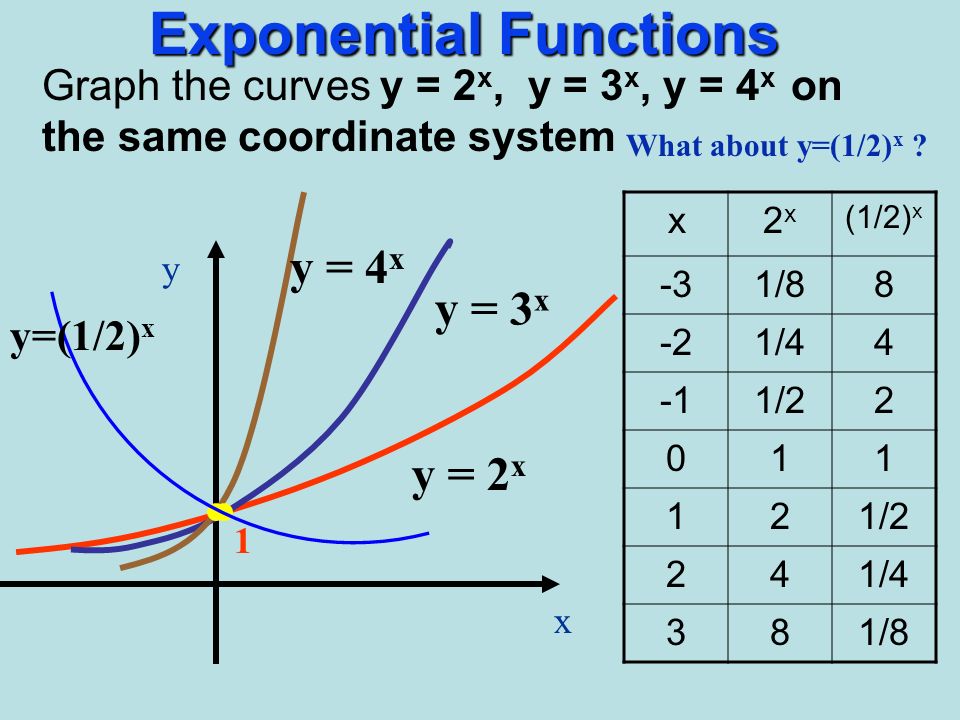


Aim What Is The Exponential Function Do Now Given Y 2 X Fill In The Table X 8 Y Hw Worksheet Ppt Download



What Is An Exponential Function Math Class 21 Video Study Com


Logarithmic And Exponential Functions Topics In Precalculus
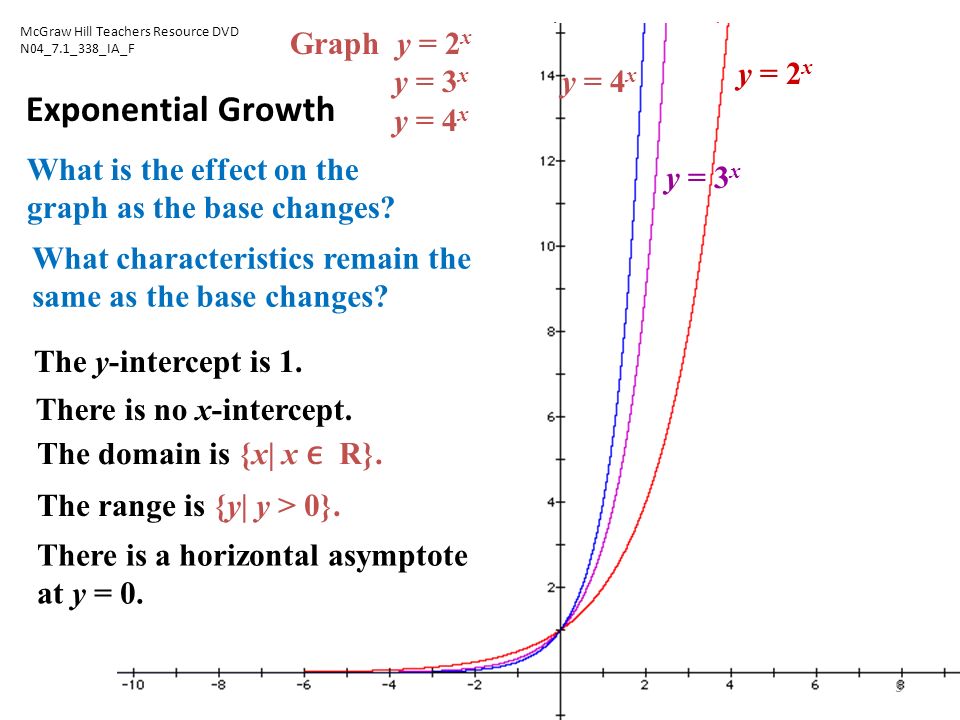


Exponential Functions Ppt Download



Write Exponential Function Decreasing With Asymptote Of 2 Y Intercept Of 5 Passing Through A Point Youtube
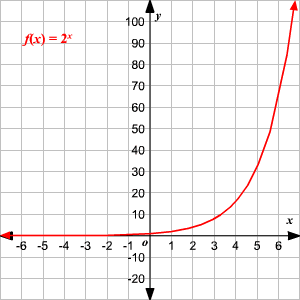


Domain And Range Of Exponential And Logarithmic Functions
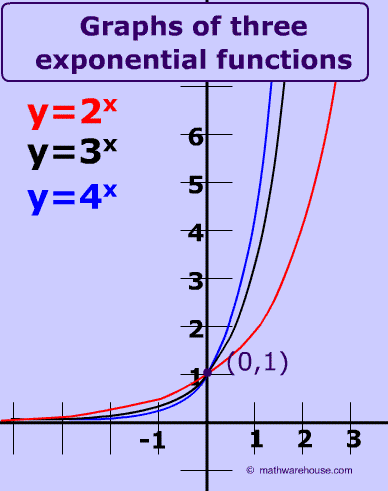


Exponential Growth Its Properties How Graph Relates To The Equation And Formula Visual Lesson Math Warehouse
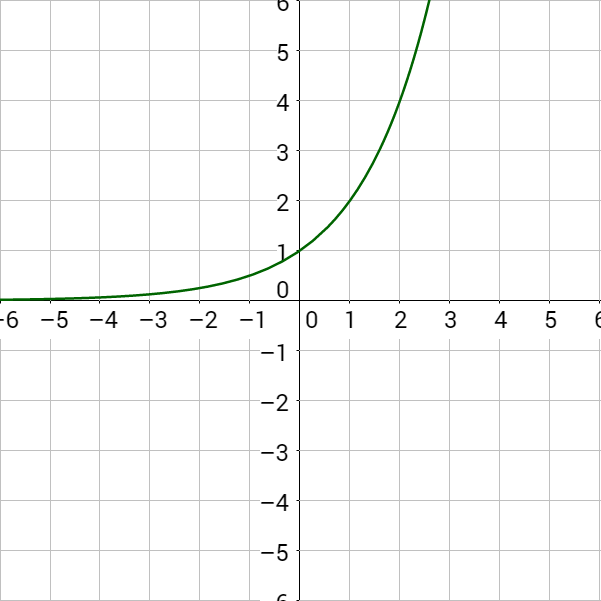


3 01 Exponential Functions


Graph Exponential Growth Functions Graph Y 4 X


Exponential Functions Mathbitsnotebook A1 Ccss Math



Solved 4 Compare With An Exponential Function 4 Points Chegg Com
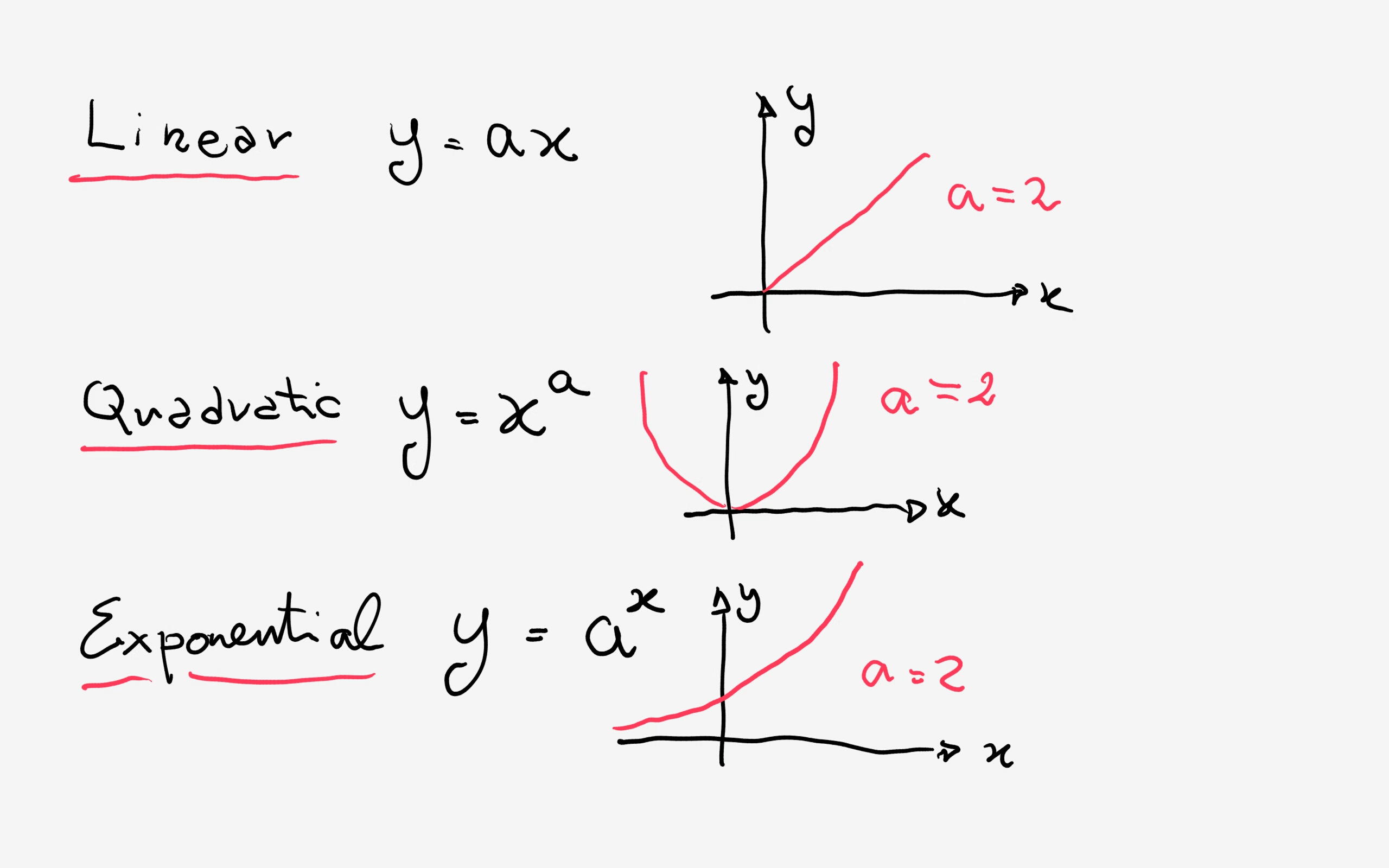


Is Y X 2 1 An Exponential Function Example


Graphing Exponential Functions



Exponential Function Wikipedia


Untitled Document


The Exponential Function Math Insight


Exponential Functions Exponential Functions Sparknotes


How To Graph And Transform An Exponential Function Dummies


Exponential Function Properties Graphs Applications
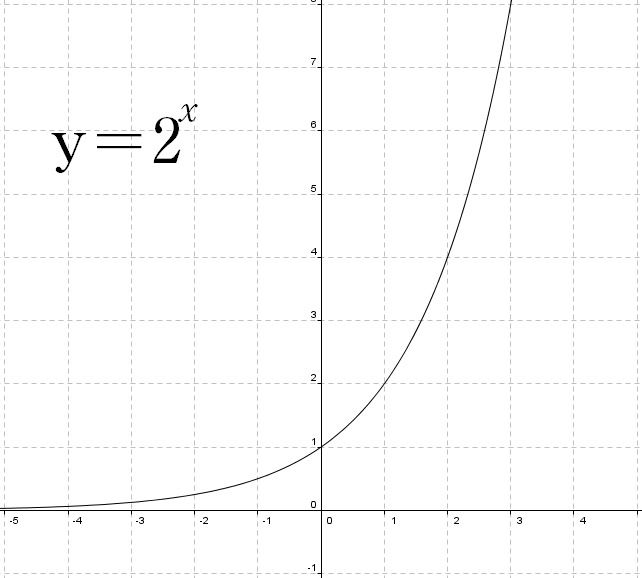


Graphs Of Exponential And Logarithmic Functions Boundless Algebra



Transforming Exponential Graphs Example 2 Video Khan Academy



Find A Possible Formula For The Exponential Function Described F 11 57 F 69 24 F X A B X Where A B Round Your Answers To Four Decimal Places Study Com
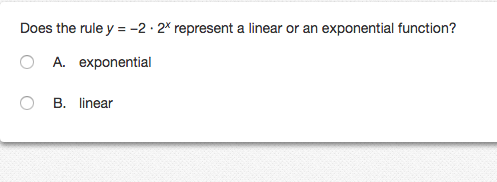


Solved Does The Rule Y 2 Middot 2 X Represent A Linear Chegg Com
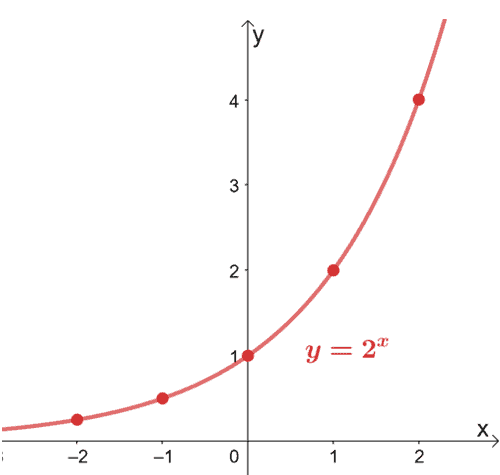


Exponential Function Properties Graphs Applications
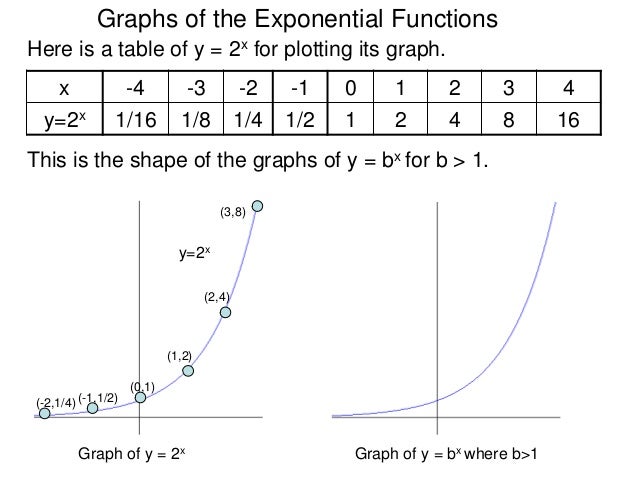


2 2 Exponential Function And Compound Interest


Exponential Function A Function With A Variable As An Exponent


Solutions 22 Graphs Of Exponential Functions Precalculus I


6 Derivative Of The Exponential Function
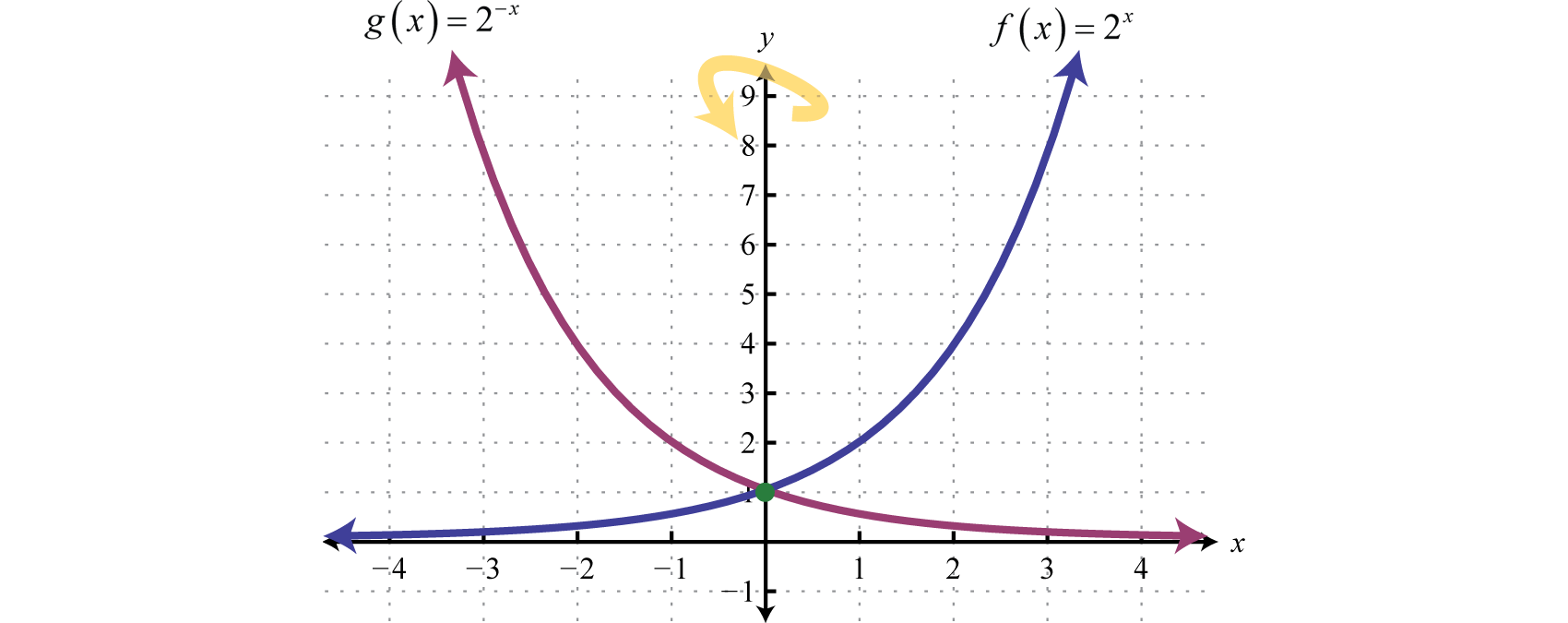


Exponential Functions And Their Graphs



The Graphs Of The Quadratic Function Y 2x 2and The Exponential Function Y 2 X Are Shown Brainly Com



What Is An Exponential Function Expii
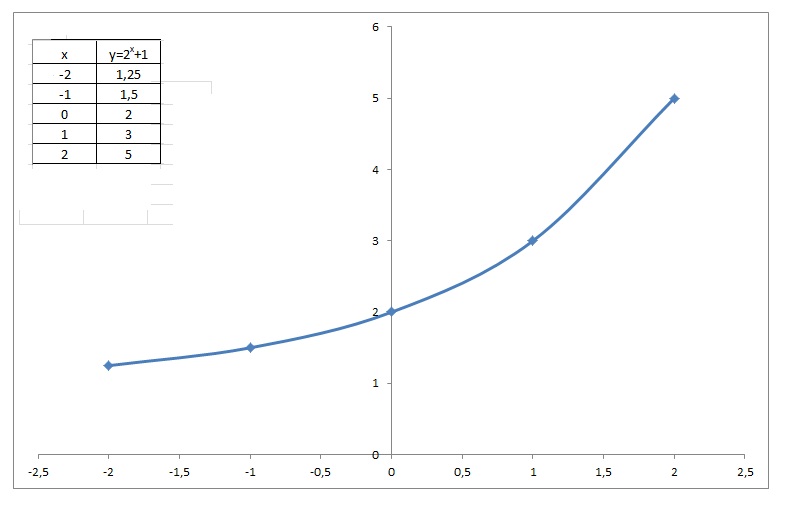


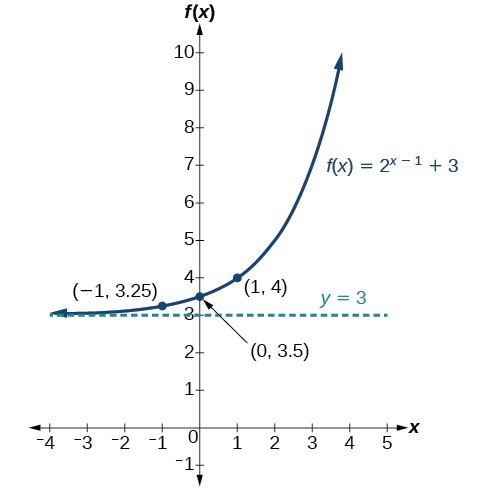
How Do You Graph The Exponential Function Y 2 X 1 Socratic


Linear Or Exponential Function
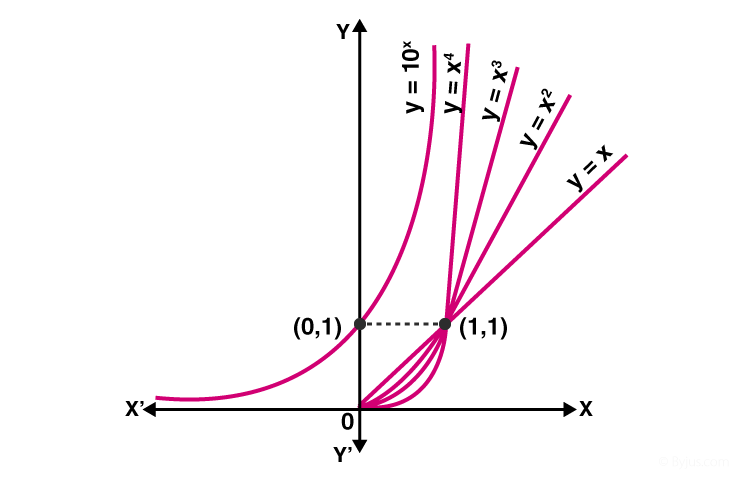


Exponential Functions Definition Formula Properties Rules
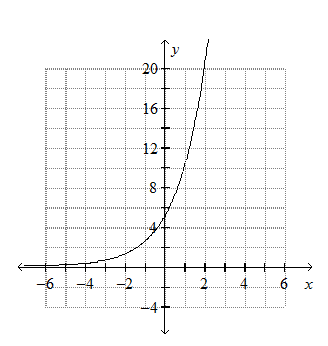


Solved Graph The Exponential Function Y 5 2 X Chegg Com


Introduction To Exponential Functions



Exponential Functions Ck 12 Foundation



Exponential Functions
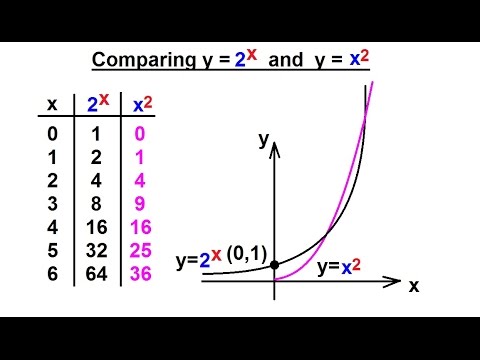


Precalculus Exponential Function 4 Of 13 Comparing Y 2 X And Y X 2 Youtube
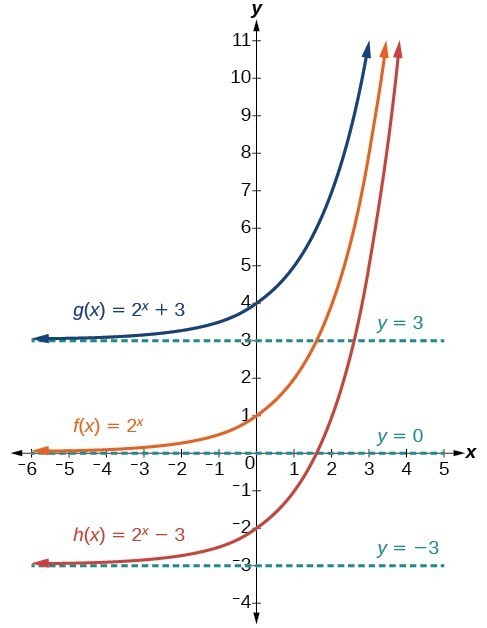


Graph Exponential Functions Using Transformations College Algebra



1 9 Limit Of Exponential Functions And Logarithmic Functions Mathematics Libretexts


Bestmaths



Exponential Functions Functions Siyavula
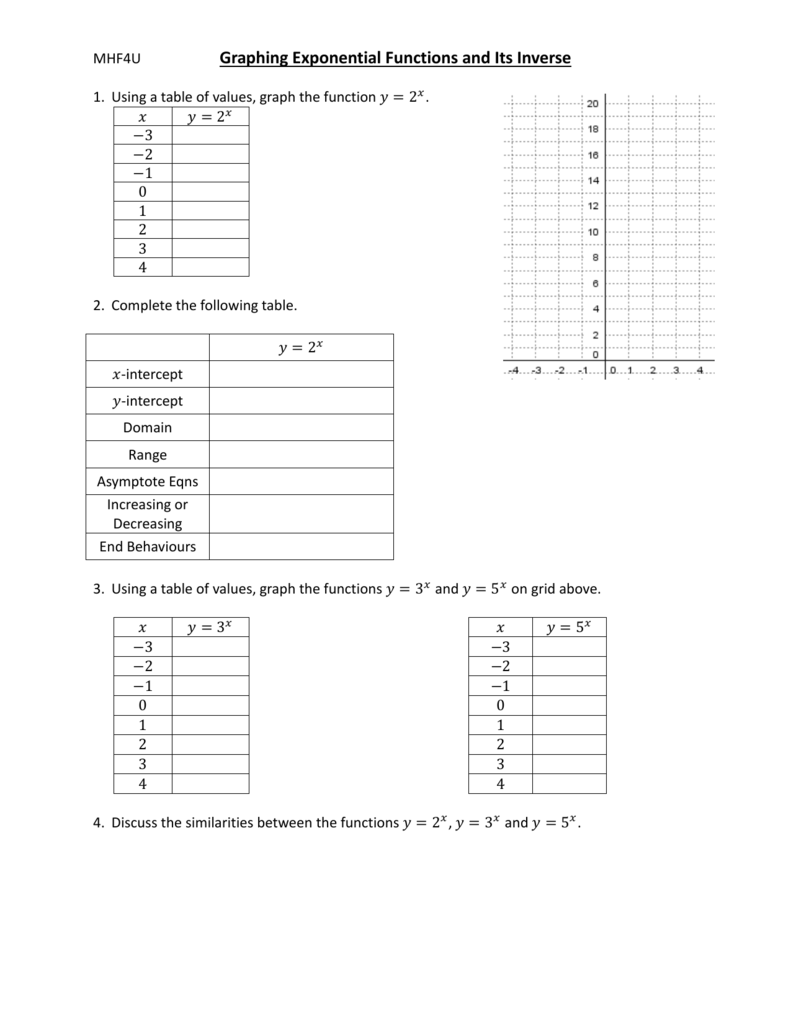


Lesson 1 Exponential Function And Its Inverse



0 件のコメント:
コメントを投稿