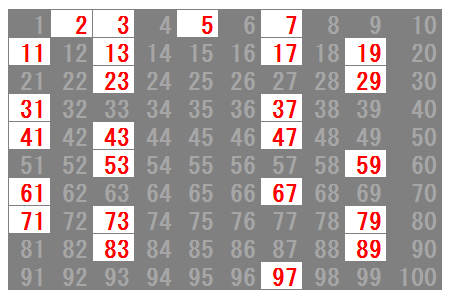
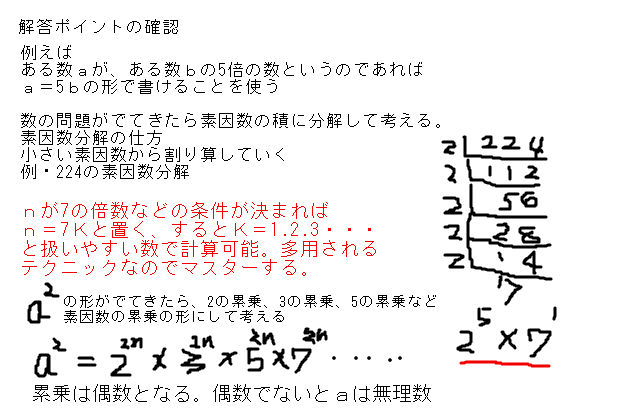
いきなりですが問題です. 「正整数nが与えられたときに,その素因数の一つを求めなさい.」は,素因数分解の関数問題です. これを参考にして,素因数分解の判定問題を答えてください. 本日の授業です.PDFの資料は前日までにMoodleに登録済みで,今日の0時に,学生が参照できもちろん素因数分解による解法なのですが・・・ この問題って、 ÷2 ÷ 2, ÷3 ÷ 3, ÷4 ÷ 4 ・・・って順に調べていけばすぐに見つかりそうです。 7 7 の約数を調べるだけですからね。 実際その解法で、ものの 1,2 1, 2 分で答えがでますね。 「1」×「その数自身」でしか表せない「数」があります このような数のことを「素数(そすう)」といいます 次に素因数分解とは「自然数」を「素数」だけの積の形( × )で表すことです この「素因数分解」を使う問題を一緒に見ていきましょう
数学の問題で 484というものが出てきたのですがどう求めたら答えが Yahoo 知恵袋
素因数分解 問題 二乗
素因数分解 問題 二乗- 素因数分解の計算問題 それでは素因数分解のやり方が分かったところで、練習問題を解いてみましょう。 答えは「最後に」を終わりの方に載せておくので、後で確認してみて下さい。 素因数分解の例題1 9を素因数分解せよ 素因数分解の例題2 18を素因数分解せよ 素因数分解の応用問題② 問「25」の正の約数の個数を答えなさい。 この問題にも、素因数分解を利用した計算式があります。 まず「 約数 」とは、 元の数をかけ算の形で表したときに出てくる数字 のこと。



素因数分解のやり方と応用問題の解き方解説
243と2772を素因数分解する問題だね。これ以上割れなくなるまで、ひたすら素数で割り算しよう。 point 各ケタの和が3の倍数なら・・・? 243を素因数分解しよう。一の位が3だから2では割れないね。ここで、以前学習した「3の倍数判定法」を思い出そう。 「各ケタの数の和が3の倍数」 ならば 手順1素因数分解をします。 手順2仲間はずれを探します。 仲間外れは です 手順3普通の問題なら をかけたものが答えですが、この問題ではどんな整数の平方になるかを聞かれているので、 に をかけたものが何の平方になっているかを答えないといけ第3①講座 素因数分解 次の中から素数をすべて選びなさい。 1,3,14,19,33,41 〔〕 次の数を素因数分解しなさい。 ⑴ 16 ⑵ 135 ⑶ 140 〔〕 〔〕 〔〕 136について述べたもののうち,正しいものをすべて選びなさい。 ア 136は2の倍数である。
単元:素因数分解 問題の解き方 問題 次の数を素因数分解しなさい。(1)(2)39(3)147(4)1230 中学生数学特訓プラン 基礎力養成特訓プラン 推奨学年中学1年~中学3年生内容計算の基素因数分解問題の性質 素因数分解は学校教育で習うように,N を 6 @N ☆4 までの素数で順に割っていくことにより素 因数分解できる.この方法を試行除算法(TD;trial division)と呼ぶ.この方法では最悪の場合に,N 以下の素数すべてについて割算を試すことになる. では,そのN以下の素数数学素因数分解 一覧 HOME 数学プリント スポンサーサイト iドリル iドリルは、中学生向けの完全無料問題を配布している学習サイトです。掲載されいている学習教材は実際に学習塾でも使用している教材で、数学・英語・理科・社会の問題のほか、入試対策問題も配布しています。 i
いやいや、この問題素因数分解なんじゃないの?素因数分解使った解法説明してよ。 と思われた方も多いと思います。 そうです、この問題は素因数分解の問題です。 この問題、本来は40を素因数分解し、17の二乗と指数法則を絡めることによって解いていくのが本来の姿なのです。素因数分解の計算 名前 次の数を素因素分解しなさい。 ① ② ③ ④ ⑤ ⑥ ⑦ ⑧ 次の問いに答えなさい。 ① はどんな数の平方か ② はどんな数の平方か ③ に出来るだけ小さい自然数をかけて、ある数の2乗にしたい。 どんな数をかければ良いか。素因数分解の問題一覧 270を素因数分解しなさい。 ・素因数分解を利用して,次の整数の約数の個数をそれぞれ求めなさい。(32 72 126) 約数の個数と素因数分解 1から30までの整数のうち,約数が4個である整数は全部で何個ありますか。 約数の個数と素因数分解 (1) 24を2でわり続けるとき何回目



素因数分解はネットの安全を守っている




中学数学3年 素数と素因数分解 受験の月
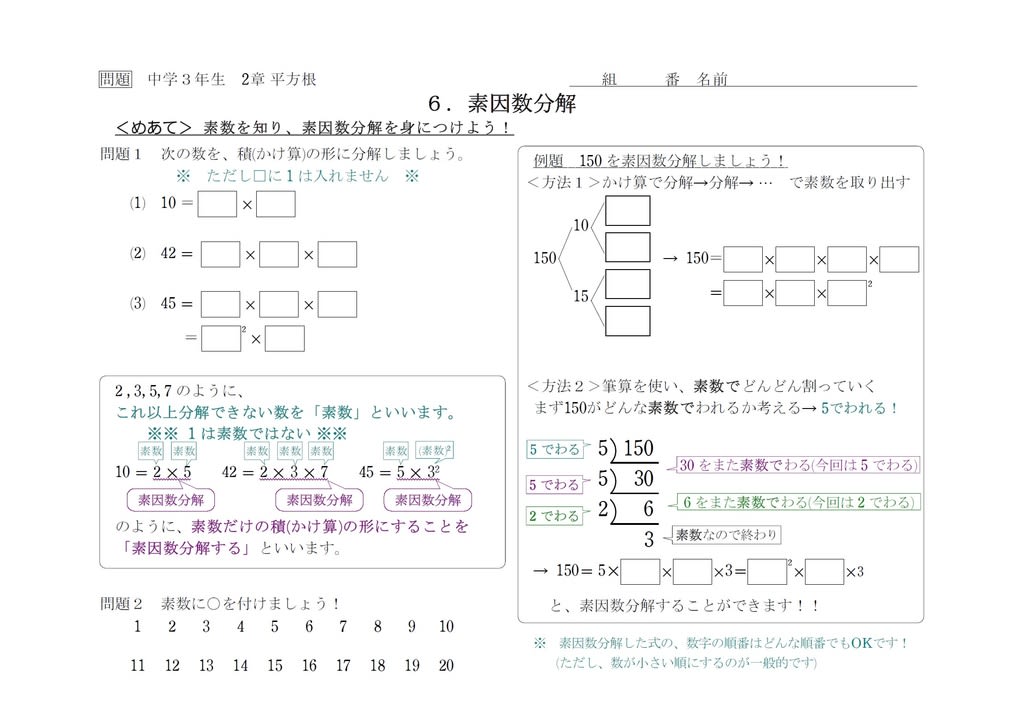
素数・素因数分解 素数 約数が1と自分自身の2つしかない自然数のことを 素数 という。 次の数のうち素数はどれか。 6, 5, 1, 0 6の約数は1,2,3,6の4つあるので6は素数ではない。 5の約数は1,5の2つだけなので5は素数である。5の部分ももう一つ掛けると2乗になる:5×5=5 2 結局,2と5を掛ければよいことになり,10を掛けることになります. ⇒10を掛けた結果は,2 4 ・5 2 =2×2×2×2×5×5= 2 となっての2乗になっています. このように,与えられた数にできるだけ小さい正の整数をかけて,ある整数の2乗となるようにするには (1) もとの数を素因数分解する (2) 各々の素因数の指数 (肩に素因数分解問題とは、整数 n( > 1)が与えられた時、n = pq となるような 1 より大きな整数(素因数)p、q を求める問題である。 111 素因数分解問題の解法 素因数分解問題の主な解法を表11 に示す。 表11 素因数分解問題の主な解法;




しょうちゃん 公式ブログ 算数の問題を解いてみる その52 素因数分解 Powered By Line
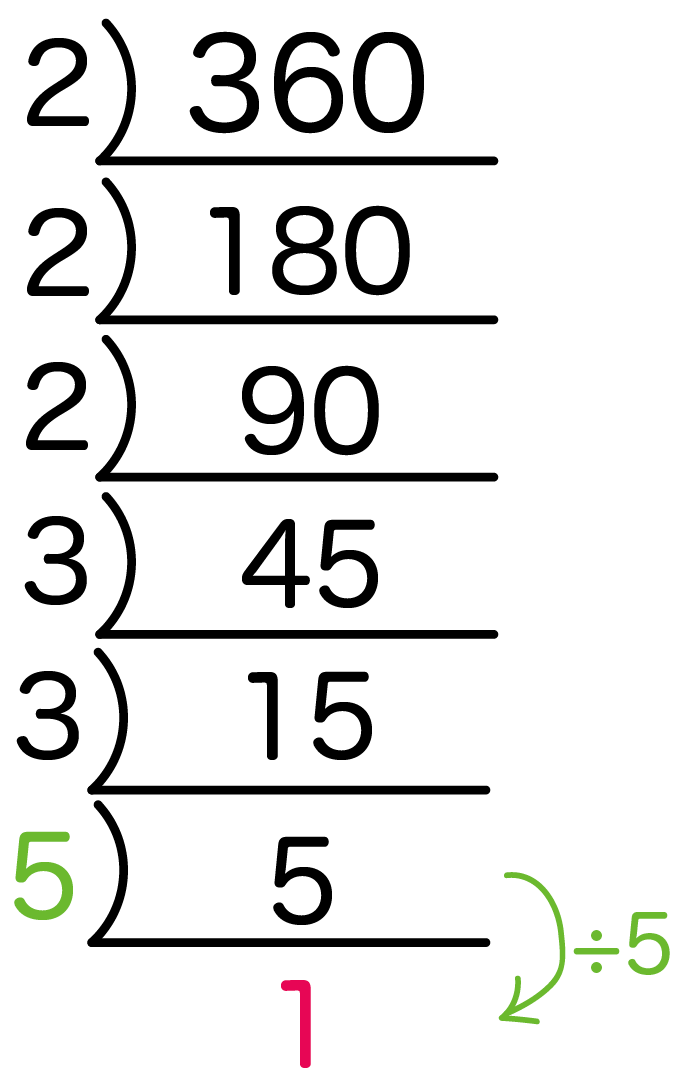



簡単計算 素因数分解のやり方 解き方がわかる5ステップ Qikeru 学びを楽しくわかりやすく
このように、 2 と 3 と 5 の素因数の見つけ方を知っているだけで、素因数分解はかなりカンタンになります。 また1 ~ 100 までの素数を覚え、これらの解き方をマスターすれば問題を解くスピードもきっと向上するはずです。5桁の数字を素因数分解したかったのですが、一目見てわかる気がしない3桁の素数2つの乗だったので大変助かりました。どうもありがとうございました。 9 1709 歳代 / 高校・専門・大学生・大学院生 / 非常に役に立った / 使用目的 受験番号が素数であるか判使いました使いました 素因数分解の応用問題3選 さて、次に考えたいのが「素因数分解を用いる応用問題」ですね。 といっても、素因数分解は整数問題を解く上での基本中の基本となるため、下手すると 応用問題 $57$ 選!! なんて記事が出来上がりかねません。(笑)




素因数分解 無料で使える中学学習プリント




約数と倍数 素因数分解 数学a の問題 2016年度後期日程大阪市立大学理系入試問題 身勝手な主張
中学生のための数学学習支援、練習問題のダウンロード、家庭学習、定期テスト対策、受験勉強にお役立てください 次の数の平方根を素因数分解を利用して求めなさい。 324 1764 1296 次のようにすでに素因数分解した形で表された数がある。この①〜③の数について できるだけ小さい自然数 素因数分解は「素数の積」で表わさなければならないので,次のようにただ単に「積」にしただけでは素因数分解とはいえない. ×間違いの例 12=4 × 3 (← 4 は素数でない.) ×間違いの例 30=3 × 10 (← 10 は素数でない.) (1) N=pq (p≦q) のように書ける素因数分解とその応用 問題一覧 ・270を素因数分解しなさい。 ・素因数分解を利用して,次の整数の約数の個数をそれぞれ求めなさい。 (32 72 126) ・1から30までの整数のうち,約数が4個である整数は全部で何個ありますか。 (1) 24を2でわり続けるとき何回




約数の個数の求め方 素因数分解すれば一発で求まる 高校生向け受験応援メディア 受験のミカタ



入試問題予想 成立学園中学 高等学校
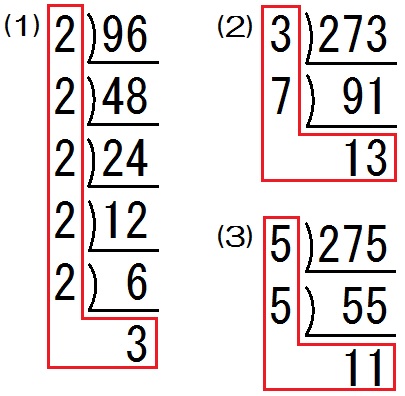
素因数分解の問題 1次の数を素因数分解しなさい。 (1)40 (2)324 (3)96 (4)400 2300 に出来るだけ小さい自然数をかけて、その結果をある整数の平方(2乗の数)にしたい。 何をかければよいか。またその結果は何の平方になるか答えなさい。試行割算法 合成数 n を小さな素数から順に割って 素因数分解の練習問題 A次の数を素因数分解しなさい。 (1)42 (2)72 (3)147 (4)387 B素因数分解することにより,次の数がどのような自然数の平方であるかを調べなさい。 (1)324 (2)676 素因数分解の解説・解答 A次の数を素因数分解しなさい。 (1) 42=2×3×7 (2) 72=2 3 ×3 2 (3) 147=3×7 2 (4) 387=3 2 ×4 3 B素因数




約数 倍数 素因数分解 問題9 公務員試験数的処理解法テクニック Komaro



Studydoctor素因数分解のやり方 中3数学 Studydoctor
1桁の整数の素因数分解の演習問題です。1桁の整数の素因数分解の演習問題に一覧があります。 下記のページには、つぎのような1桁の整数の素因数分解の演習問題が5問あります。 「8」を素因数分解してください。 >1桁の整数の素因数分解の演習問題 No1 素因数分解の問題はどこのサイトを検索すれば良いでしょうか? お願いします より 21年1月14日 253 pm 二乗して 1になる数字を筆算で求める方法を教えてください。公式など使わず(つまり公式を思い出さなくても)紙の上で、さっさと書きながら、小数点以下も必要に応じて求める方法が ずばり素因数分解とは、 自然数 を 素数 の積に分解することです。 素因数分解の「素」は素数の「素」です。 「素因数=素数」と考えて問題ありません。素数の因数を素因数と呼んでいるのです。 分解されたものを「因子」または、「因数」と呼びます。 自然数(整数の場合もあります)を素数の積で表すことを素因数分解といいます。



対数logの値を求める問題で これだけ間違えてしまったのですが出来る Yahoo 知恵袋



素因数分解のやり方を分かりやすく解説 計算問題も付いてます Studyplus スタディプラス
素因数分解と素数の問題。数学の基礎問題を中心に掲載。普段の家庭学習や定期テスト・受験勉強に! 中学生 勉強なんて 怖くない ~ 勉強が苦手な中学生のために ~ TOP > 中学3年 数学 練習問題一覧 > 因数分解(1) ‐ 素因数分解 勉強しないで後悔するくらいなら、 後悔してもいいから素因数分解とは、「 素数のかけ算にガンガン分解する 」ことだったね。 ポイントをよく見直しながら、問題を解いて慣れていこう。 まずは 2とか3とか、小さい数で割り切れないかどうか 調べていく約数・倍数・素因数分解問題1 約数・倍数・素因数分解問題2 約数・倍数・素因数分解問題3 約数・倍数・素因数分解問題4 約数・倍数・素因数分解問題5 約数・倍数・素因数分解問題6 約数・倍数・素因数分解問題7 約数・倍数・素因数分解問題8




素因数分解のやり方のコツとは 応用問題3選も簡単に解けます 遊ぶ数学




素因数 分解 と は 競プロ 素因数分解 Amp Petmd Com
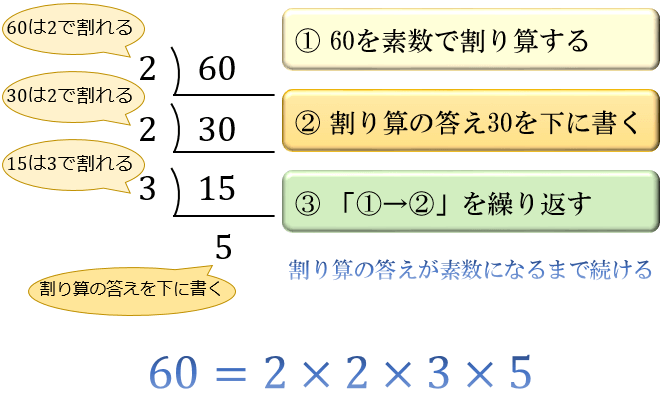
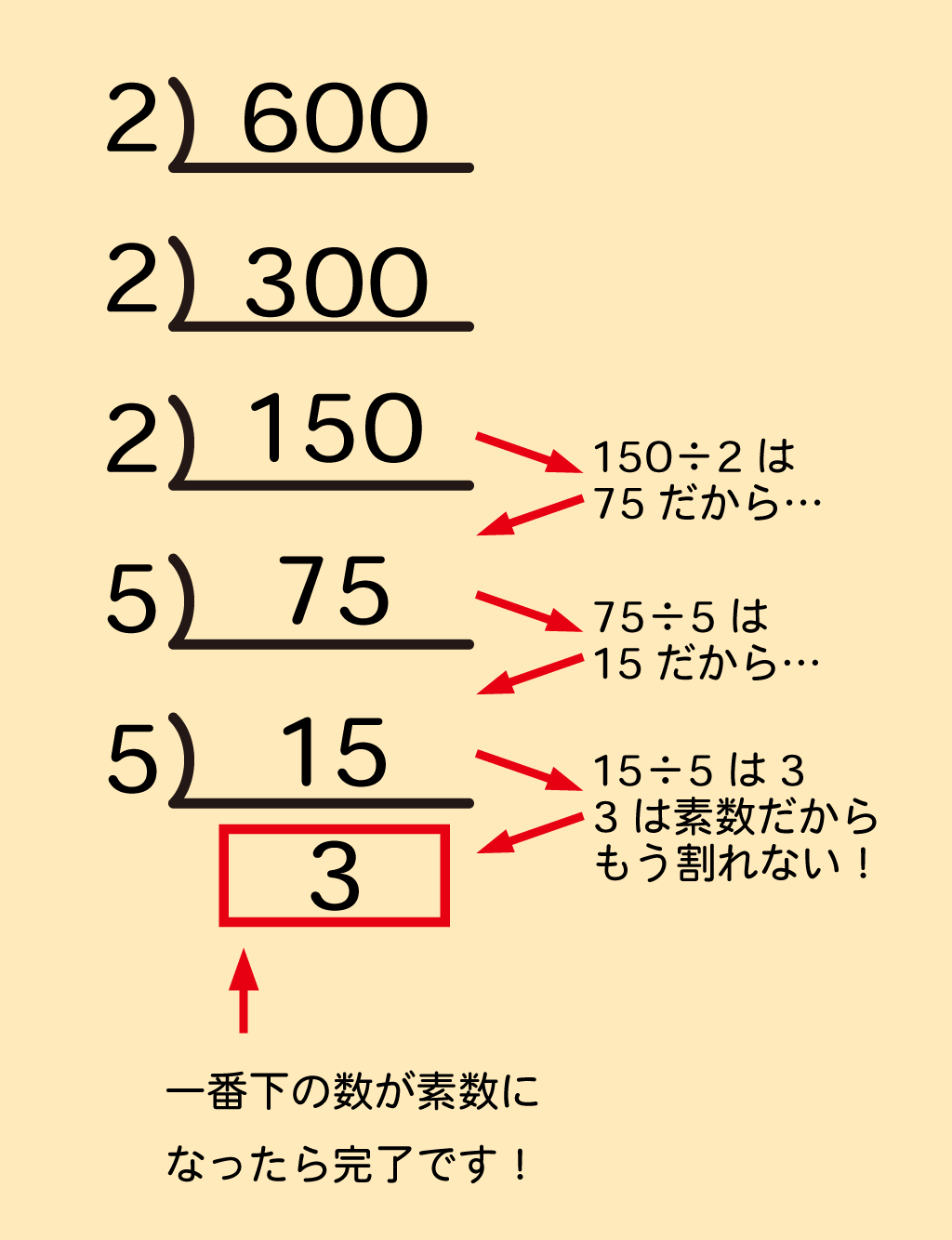
素因数分解可能な範囲 04年現在、インターネットで公募した数多くのpcを用いると512ビット程度の数なら素因数分解できる。 したがって、現在では、rsa暗号に使用する法 n をビット(10進数で桁程度)にすることが推奨されている。解説 ある数が3の倍数か否か、5の倍数か否かについては、どちらもすぐに判定できるので、7の倍数から確定させます。 (7の倍数-1)が5の倍数になるためには、7の倍数の1の位が1か6です。 そのような7の倍数と、その手前の数2つを書きだします。 3段目このように自然数を素数の積に分解することを素因数分解という。 素因数分解の考え方 素数になるまで、小さい素数で順にわっていく。 2)12 ←素数2 で割る 2) 6 ←素数2 で割る 3 ←素数 基本問題 次の数を素因数分解しなさい。



この問題で素因数分解した後によって有理数となるのは と書くのは Yahoo 知恵袋



中学3年の数学 動画 素数と素因数分解の問題 19ch
素因数分解に慣れよう! 表示された数字を、割り切れる素数で割っていこう。 2~13のボタンをタップして、 数字が1になるまで 割っていきましょう! 割り切れない数字を選ぶと、先に進みません。 最後までできてもできなくても、「 別の問題に挑戦 素因数分解の練習です。素因数として、2,3,5,7が考えられるような数が並ぶので、すだれ算などを駆使して、素数の積の形にしてください。 中学受験では必須の内容です。約分や割り算の計算練習としても優れています。 経過 09年10月23日 素因数分解1素因数分解の活用 整数問題が面白いほどわかる 整数問題が面白いほど分かる #2このシリーズは受験生を最も悩ませる整数問題を基礎



数学の素因数分解の問題の答え方ですが 弟がこうやって書きました 計算 Yahoo 知恵袋




中3数学 素因数分解とは 練習編 映像授業のtry It トライイット




素数 素因数分解の問題です Clear



素因数分解のやり方 5つのステップで分かる素因数分解問題の解き方とコツ アタリマエ




中学3年生 数学 因数分解 問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生
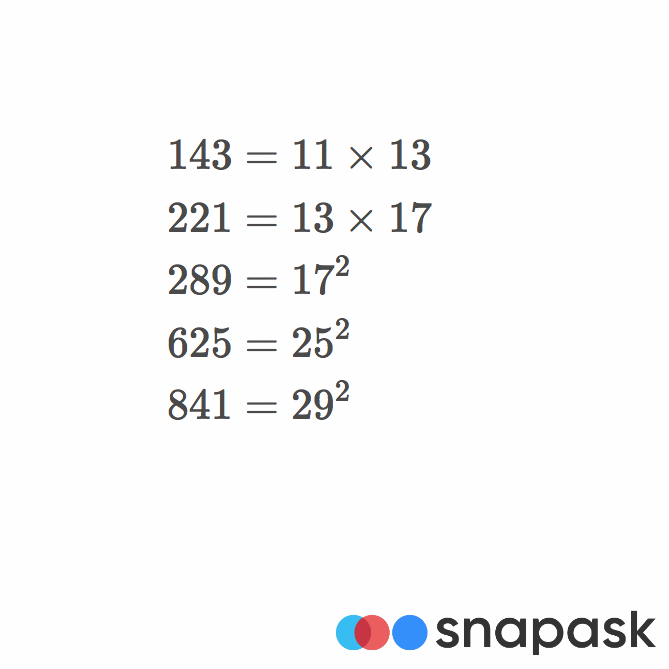



個別指導アプリ スナップアスク 本日の問題 本日は素因数分解です 一の位に着目して考えてみると思いつくと思いますよ 中学数学 数学 受験生 受験勉強 高校受験




Javaの簡単な問題 3 素因数分解 T Nakaの阿房ブログ



2
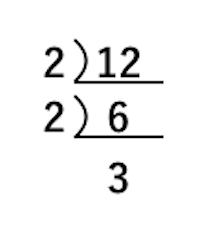



簡単にできる素因数分解 苦手な数学を簡単に



U9j580gf8iba369ji2w Xyz P 1542




素因数分解の質問です Clear




素因数分解の応用問題 難問 中学数学 理科 寺子屋塾の復習サイト




素因数分解の問題 Youtube



中3数学 基本解説 問題 308 式の計算8 素因数分解 プリント




2021を素因数分解せよ セルモ大蔵 世田谷 の塾長ブログ




展開 因数分解を利用した計算の工夫 無料で使える中学学習プリント



素因数分解のドリル




中学3年生 数学 因数分解 問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生



数学の問題で 484というものが出てきたのですがどう求めたら答えが Yahoo 知恵袋




素因数分解の利用問題なのですが 2が4乗されているのはそのままで良い のがよくわかり Clear




中学数学 平方根 整数になる自然数n の簡単なやり方 丁寧な解説 スタディーランナップ




因数分解で大活躍 倍数 約数 の見つけ方




素因数分解の応用問題の解き方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく



素因数分解のやり方を分かりやすく解説 計算問題も付いてます Studyplus スタディプラス
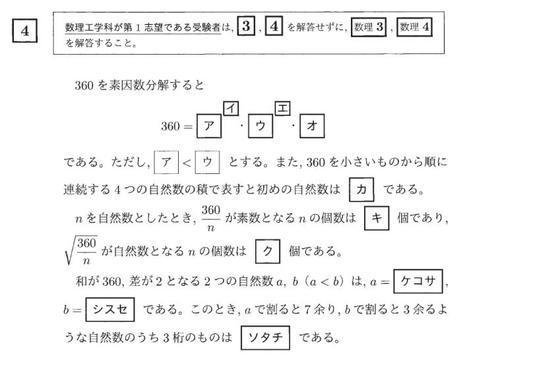



既約分数に関する整数問題です 大学入試数学問題の解説 解答




中3 数学 素因数分解 無料学習プリント教材



3




素因数分解のプリントは 小5も中3も同じです 算数 数学専門塾 算数の極意




素因数分解で平方因数を外に すうがくのいえ




中3 中3数学 式の計算 素因数分解と因数分解 中学生 数学のノート Clear



1




高校数学a 素因数分解とは 練習編 映像授業のtry It トライイット




素因数分解のやり方と応用問題の解き方解説




素因数分解とは 素因数分解のやり方を練習問題と解説でマスターしよう 高校生向け受験応援メディア 受験のミカタ
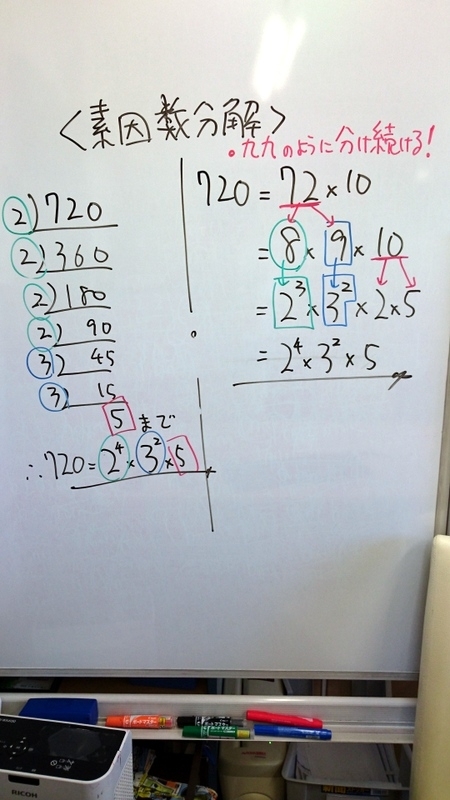



1 中学時のやり方を捨てよ 7 を10秒で素因数分解する方法 塾講師 加藤哲也 マイベストプロ岐阜




素因数分解のやり方 簡単な問題を素数で割ってみよう 中学や高校の数学の計算問題
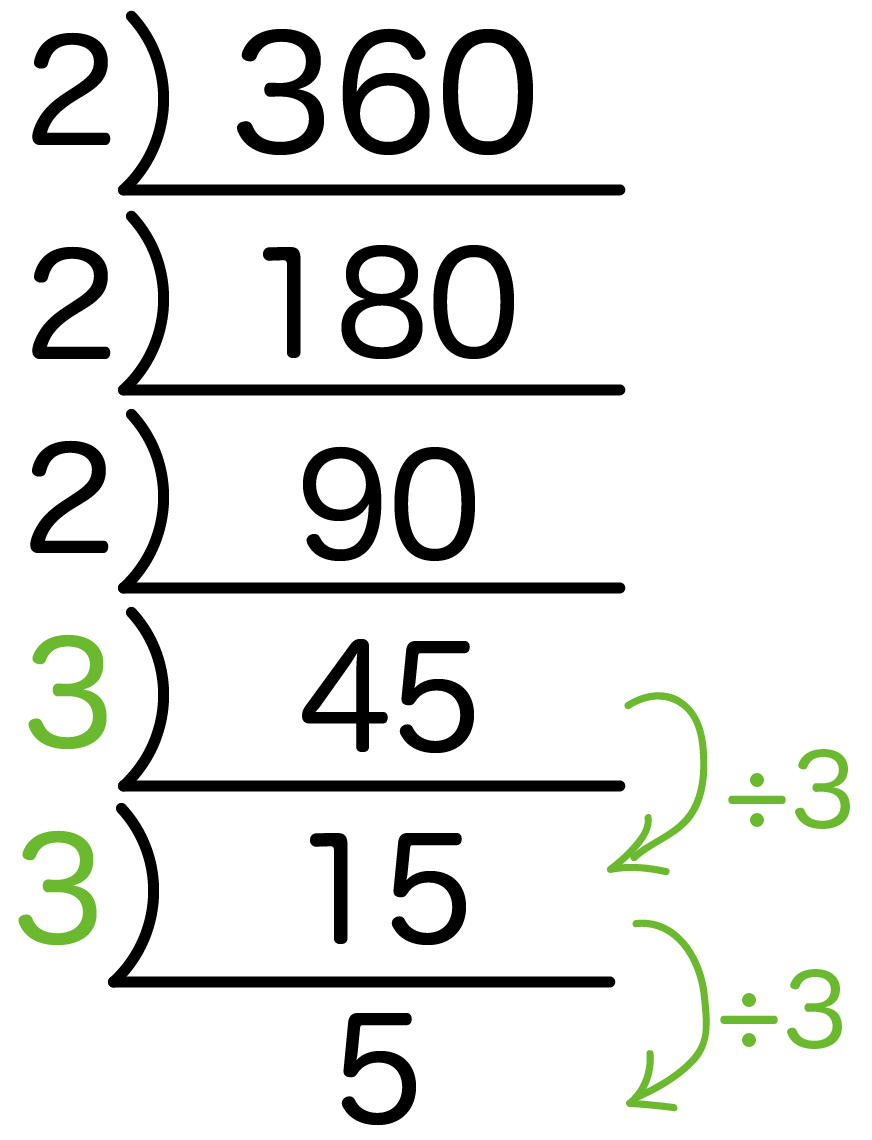



簡単計算 素因数分解のやり方 解き方がわかる5ステップ Qikeru 学びを楽しくわかりやすく




中3の素因数分解を利用した応用問題なのですが Clear




素因数分解が難しい日付19選 素数選 Sosu Lover Number Mania Note




中3数学の計算問題プリント 因数分解 桜花 現役バイト塾講師 Note




素因数分解 問題解答自動作成 授業で使える教材倉庫




中3数学の素因数分解の問題 N2乗 24 N2乗 18がともに自然数になるnとは メモ帳



中学数学 平方根 のコツ 素因数分解 ルートを簡単にする計算



Q Tbn And9gcrtko3yfy9v51cbohja5dd2sdxucibzvsnbdf9rrnkzeb8hboz Usqp Cau




競プロ 素因数分解と約数と倍数 なかけんの数学ノート




天才ドリル 素因数パズル 小学校3年生以上 算数 考える力を育てる 認知工学 本 通販 Amazon



中学3年生向け 平方根はこうやって解く 平方根を基本から徹底解説 学習内容解説ブログ




高校数学で整数の素因数分解から約数の総和を樹形図で学び直し 大学受験対策にも タロウ岩井の数学と英語 Note




問題 素因数分解を利用して 126の約数を求めよ 126 2 3の2乗 7 Clear




問題解説 センター試験平成30年度本試験 Ia 第4問 数学が好きなサラリーマンのブログ



至急 中1の素因数分解の問題について教えて下さい Yahoo 知恵袋



中3 平方根6 素因数分解 中学数学の勉強に



素因数分解の応用問題 中学数学 理科 寺子屋塾の復習サイト




天才ドリル 素因数パズル 小学校3年生以上 算数 考える力を育てる 認知工学 本 通販 Amazon




Project Euler 3 Pythonで数学系の問題を解いてみた 素因数 きまびぎ



2




無料 中3数学 標準問題 解答プリント 304 式の計算4 素因数分解




素数雑感1 素因数分解の一意性 身勝手な主張



中3数学 式の計算8 因数分解 発展問題 問題 308 プリント




素因数分解のやり方 簡単な応用問題 数学の偏差値を上げて合格を目指す




中学3年生向け 平方根はこうやって解く 平方根を基本から徹底解説 学習内容解説ブログ



84の素因数分解の問題で 問1 できるだけ小さい自然数をかけてある数 Yahoo 知恵袋



3



素因数分解の筆算 Wordで数学問題プリントを作ろう




素因数分解の利用 Youtube




算数 数学 21年問題について考える 素因数分解 Aで学びたい高校のnote塾 Note




中1 1学期 整数の性質 素因数分解 のわかりやすい教え方 教える手順 ノートのとらせ方 問題もあります ヒカリブログ ワーママhikariの目からウロコ




15年前期 千葉県公立高校入試 数学 第2問 2 素因数分解の発想の応用 船橋市議会議員 朝倉幹晴公式サイト




この問題の答えはルート42なのですが 私の答えでは ですか Clear




素因数分解のやり方 Youtube
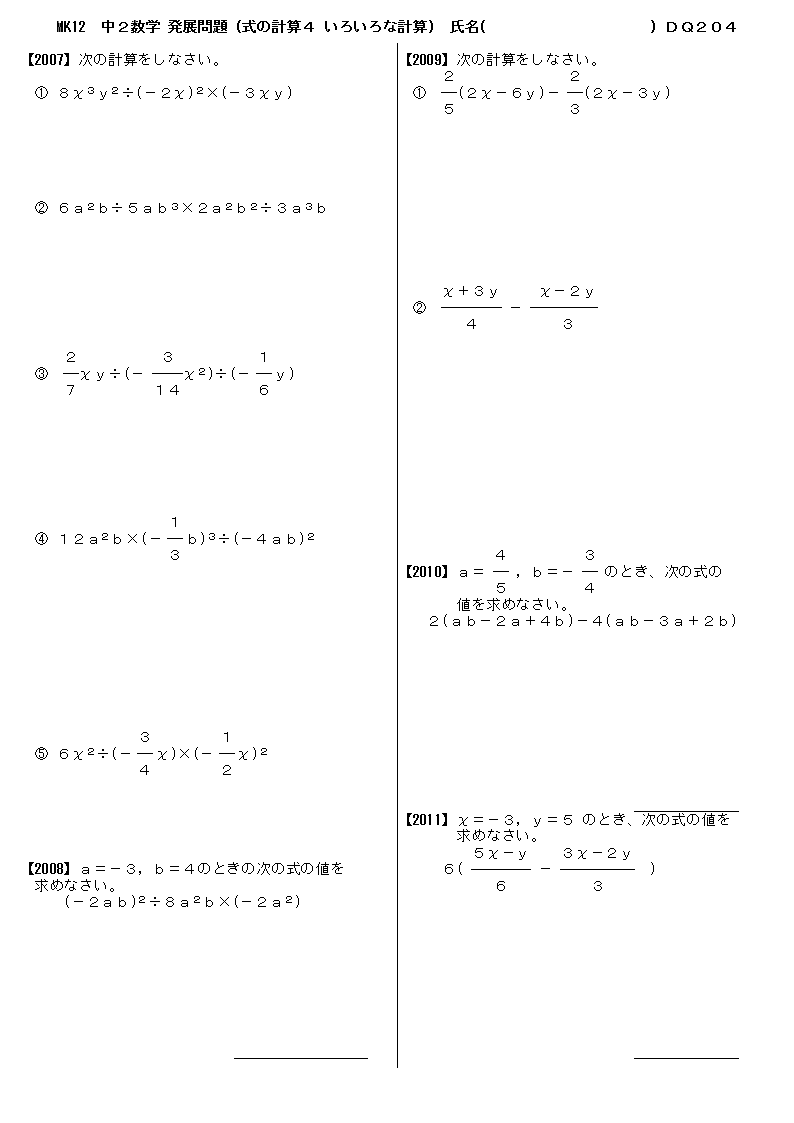



無料 中2数学 応用 発展問題 問題プリント 304 式の計算4 素因数分解




素因数分解の問題です 解説見てもわかりませんので Clear



これで大丈夫 素因数分解のやり方と応用



2



中3数学12 式の計算4 素因数分解 基本問題プリント 問題 304




素因数分解の応用問題の解き方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく




素因数分解 ある自然数の2乗になるためには 何をかける わる Youtube




数学 中3 5 素数と素因数分解 Youtube



面白クイズ 9991を素因数分解




第20回約数と公約数 素数と素因数分解 問題 スタディカフェ




中学数学3年 素因数分解の応用 約数の個数 平方数 受験の月



中3数学12 式の計算4 素因数分解 標準問題プリント 問題 304




世界一わかりやすい数学問題集中3 1章 式の展開と因数分解
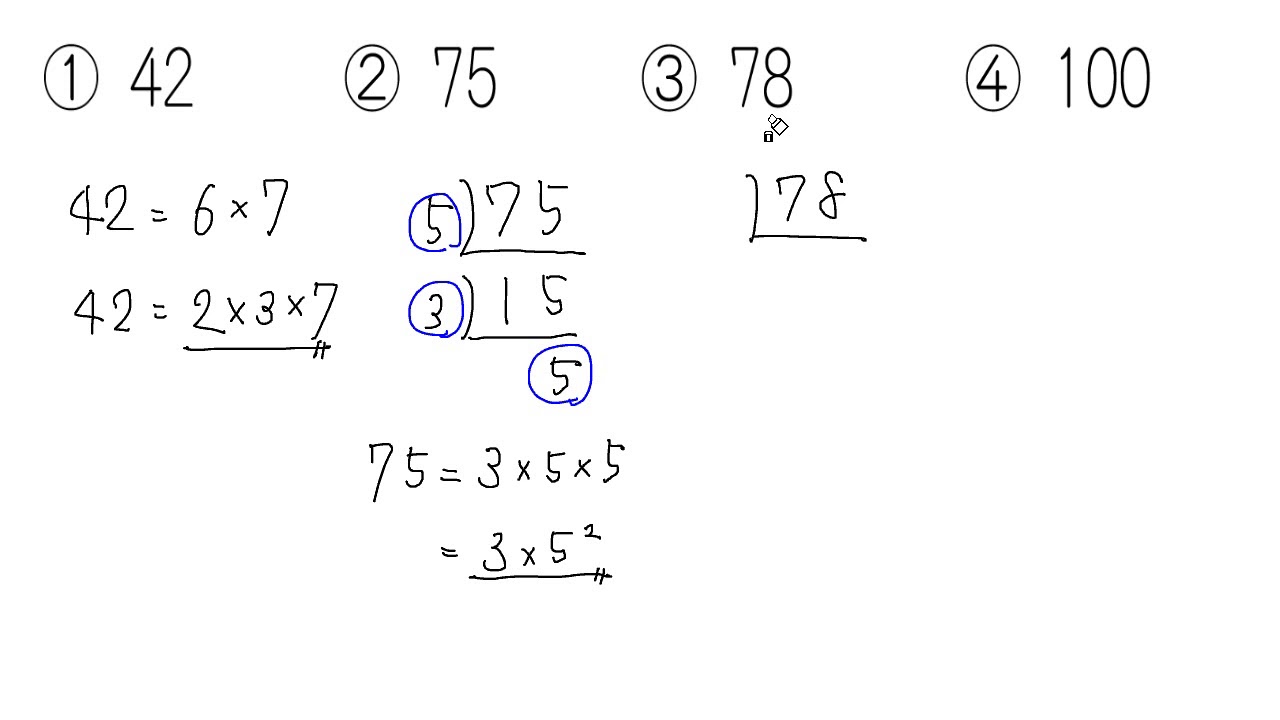



素因数分解 問題 Youtube




300の約数を求めよ という問題で 素因数分解を利用してとく方法に Clear




中学数学 因数分解 素因数分解のわかりやすい解説 入試問題 数学の面白いこと 役に立つことをまとめたサイト




素因数分解を利用する応用問題の解き方 現役塾講師のわかりやすい中学数学の解き方



素因数分解とは やり方やコツ 利用問題 約数など 受験辞典



0 件のコメント:
コメントを投稿