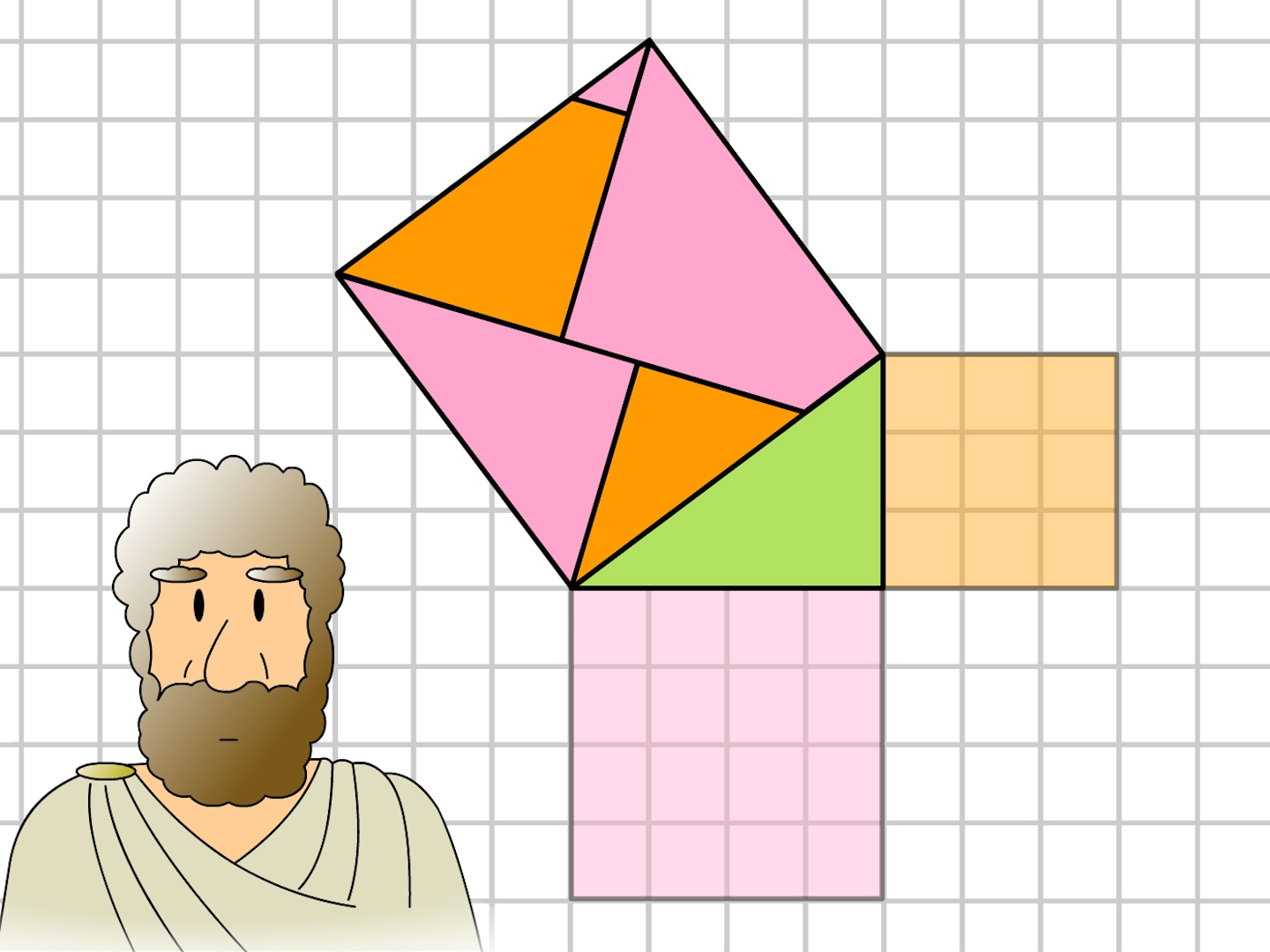
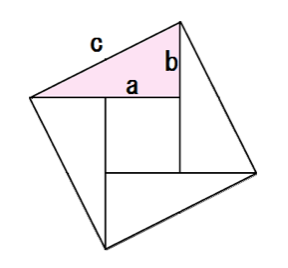
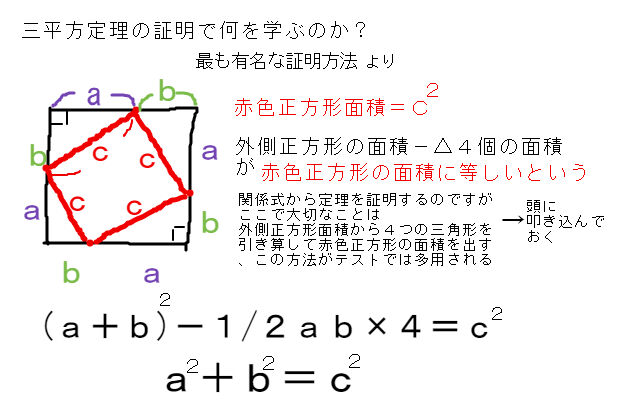
三平方の定理とは、古代ギリシアの数学者である「ピタゴラス」の名前を取って、「ピタゴラスの定理」と呼ぶこともある定理で、「直角三角形の3辺の長さの関係」表す定理です。 直角三角形とは、中学数学で散々見てきた これですね。 2辺が直角 (すなわち90°)となるように接し、その2辺の端を繋ぐ斜めの線を付けることで完成するこの図形、この長さの関係は実は三平方の定理によって決まっ
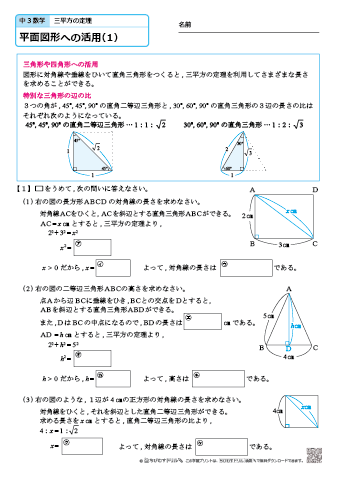
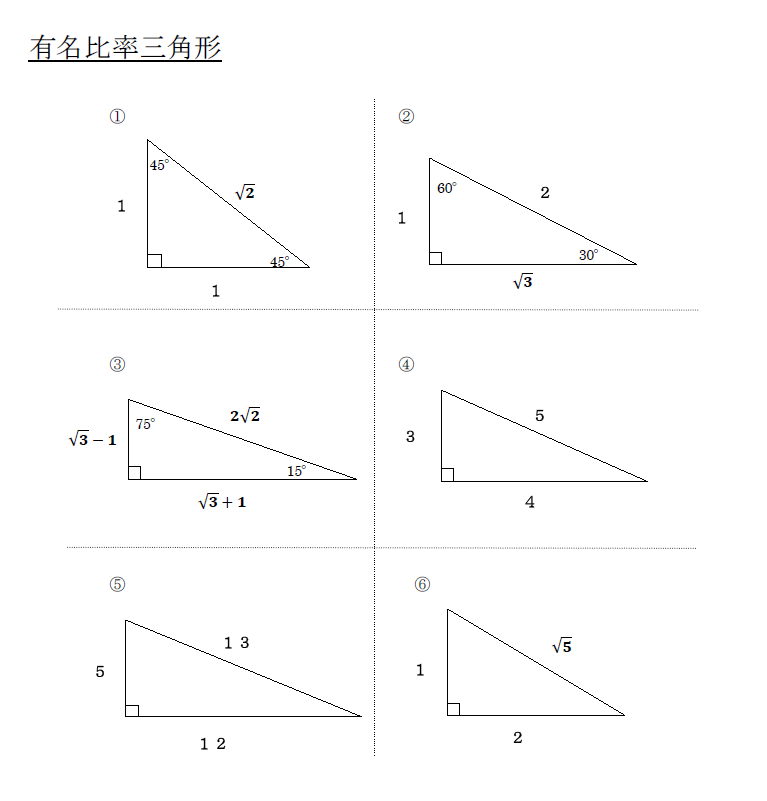
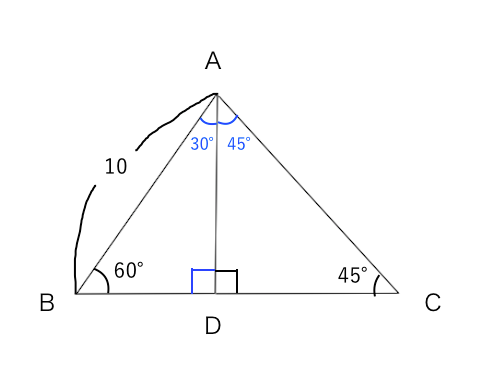
三 平方 の 定理 中学- 中3 学習単元一覧 式の展開 因数分解 平方根 2次方程式 2乗に比例する関数 図形の相似 三平方の定理 円の性質 標本調査 式の展開式の展開の基礎乗法公式1乗法公式2三平方の定理 特別な直角三角形の3辺の比 中学生からの質問(数学) や が出てくるのは,次の2つの特別な直角三角形の場合です。 直角三角形においては三平方の定理が成り立つため,3つの角が30°,60°,90°である直角三角形と,45°,45°,90°である直角三角形の3辺の長さには,それぞれ次のような関係が成り立っています。 特別な直角三角形の3辺の比 30°,60°,90°の 直角三角形
三 平方 の 定理 中学のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 |  |  |
 |  |  |
 |  | |
 |  |  |
「三 平方 の 定理 中学」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
 |  | |
「三 平方 の 定理 中学」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 | ||
 | ||
「三 平方 の 定理 中学」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 | ||
 |  | |
「三 平方 の 定理 中学」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  |  |
 |  |  |
「三 平方 の 定理 中学」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  | |
 |  |  |
「三 平方 の 定理 中学」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  |  |
 |  |  |
「三 平方 の 定理 中学」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  |  |
 |  |  |
「三 平方 の 定理 中学」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  |
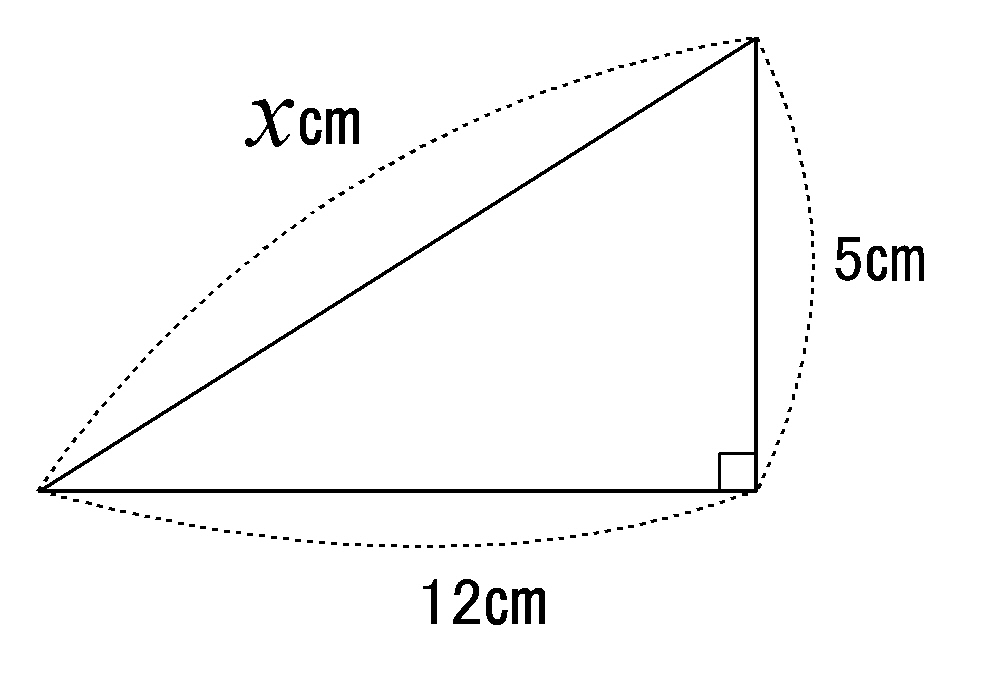
三平方の定理が使えるのは直角三角形である。 定理を利用する場合は図から直角三角形を探すか、補助線を書いて直角三角形を作る。 座標上での2点間の距離 いままで、座標上で斜めの長さは出せなかったが、三平方の定理を使えば出せるようになる。 A B 例図の線分ABの長さを求める。 x y O A (2,1) B (7,3) 確認線分ABの長さを求めよ。 A (1,5) B (6,2) x y O B (2,2) A (1, 4) O x y 長方形三平方の定理より、 2 2 +高さ 2 =12 2 高さ 2 =140 高さ=± 140





0 件のコメント:
コメントを投稿